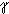plati:
a+ß+= 
.
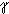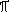Urcte maximum vyrazu: sin a+ sin ß+ sin .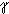
Geometricke odhady
1.Aky maximalny pocet gul priemeru 1 mozno vlozit do krabice tvaru kvadra s rozmermi 10x10x1? Staci udat pocet a rozmiestnenie gul.
2Pre uhly a, ß, 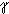plati:
a+ß+= .
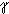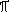Urcte maximum vyrazu: sin a+ sin ß+ sin .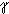
3.V rovine je danych sest bodov tak, ze vzdialenost medzi lubovolnymi
dvoma z nich je aspon 1. Dokazte, ze vzdialenost niektorych dvoch z nich
je aspon (1+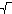 
6)/2.
4.Na stranach AB,BC,AC trojuholnika ABC su dane po rade body P,Q,R. Dokazte, ze plocha aspon jedneho z trojuholnikov APR , BPQ , CRQ nie je vacsia ako 1/4 plochy trojuholnika ABC.
5a.Odohrava sa namorna bitka pri Liparskych ostrovoch. Kontraadmiral Bourbaki na parniku Korinthos smutne sledoval (dalekohladom) svoje posledne dve bojaschopne plachetnice. V rozhodujucom okamihu plachetnice a admiralsky parnik tvorili vrcholy rovnostranneho trojuholnika so stranami 5 mil. Bourbaki chce v co najkratsom case sustredit svoje lodstvo. Kam ma zvolat plachetnice, aby sa tri lode (dve plachetnice a parnik) stretli v co najkratsom case, ked rychlost plachetnic je 1/2 rychlosti parnika a je nezavisla na smere plavby (zakrivenie Zeme neuvazujeme)?
5b.Rieste ulohu 5a. a navyse pripad, ked rychlost plachetnic je 0.9 nasobok rychlosti parnika.