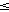1.Nech f je lubovolna funkcia definovana na mnozine vsetkych prirodzenych cisel (postupnost). Potom existuje rastuca funkcia g a klesajuca funkcia h --- obe definovane na mnozine prirodenych cisel tak, ze pre vsetky n plati: f(n)=g(n)+h(n) . Dokazte.

2.Oznacme [x] take cele cislo, aby: x-1<[x]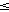 x (tj. cela cast cisla x)
Nech h(x)=[x/2]+[x/4]+[x/8]+...+[x/128] . Najdite vsetky nN mensie ako 1111, pre ktore bude platit: h(n+1)-h(n)=7.

3.Nech g je funkcia definovana pre vsetky realne cisla. Ak plati: g(g(g(c)))=c a sucasne bude platit: g(g(g(g(g(c)))))=c pre nejake cR, potom aj g(c)=c. Dokazte.

4.Nech f(x) je funkcia definovana na R, ktora nie je identicky rovna 0. Nech pre 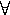x, yR plati: f(x).f(y)=f(x-y). Urcte funkciu f(x) .

5.Na intervale < 0,1 > su dane funkcie S(x)=1-x a T(x)=1/2x. Najdite funkciu tvaru f=g₁o g₂o...o g_n, kde nN a cinitele g_k pre k=1, 2,...,n su same S(x) alebo T(x), pre ktoru f(1/2)=19/32 . (g₁o g₂ znaci funkciu zlozenu z funcii g₁, g₂)

Sisler, Jarnik: O funkcich - SMM 4
Smital: Funkcionalne rovnice