FACULTY OF MATHEMATICS & PHYSICS OF COMENIUS UNIVERSITY
UNION OF SLOVAK MATHEMATICIANS & PHYSICISTS
CENTRE OF SPARE TIME - IUVENTA

BMCS - Official solutions for the 2nd fall series 1997/98

Triangles

  1. Let's construct any triangle A'B'C' with angles a, ß, 180-a-ß. A'B'C' is homothetic with the triangle ABC and therefore (tb'+va'+R')/(tb+va+R) is the coefficient of homothety. The length of |AB| is sufficient for us to be able to construct the triangle ABC. We will get it by the following (standard) procedure: We plot the geometric sum of lengths |va'|+|tb'|+|R'| on the ray AX of an arbitrary angle XAY and the given length va+tb+R on the ray AY. We mark the end points as X1 and Y1. Now we plot the point B' on the ray AX in the distance |A'B'| from A. We construct a line B'Z - to be parallel with X1Y1. Intersection of B'Z with AY is the point B. The rest of the construction is a standard triangle construction (angle, side, angle).

    Discussion: There exists exactly one solution for 0 < tb+va+R and a, ß < 180 o and no solution otherwise.

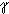  2. Let the feet of heights of the triangle are Va and Vb, r is the radius of the circumscribed circle of the triangle ABC and is the angle ACB.
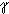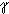    Let |XYZ| denotes the size of an angle XYZ. Then
    |CAVa| = |VaAD| = 1/2 . |BAD| = 90 o-.
    We know from the periphery and central angle properies that |ASB|=2.|ACB|=2.. Because |AS|=|BS|, then necessarily |BAS|=90 o-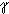. Then |SAD|=|BAD|-|BAS|=90 o-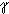. It is evident now, that |SAD|=|VaAD|. OS is perpendicular to AD (where O lies on AVa). Consequently, |AO|=|AS|. We will express the length |AO| and |AS| using the sine theorem in the triangle ABVb and ABC, respectively:
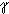    |AO| = (|AVb| / sin = 1 / sin 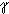. ( (c.sin(|ABVb|)) / (sin(|AVbB|)) ) =
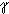    = (c.sin(4. - 270 o)) / sin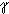

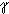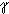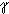    |AS| = r / 2 = c / (2.sin)
    and thus
    1 / 2 = sin(90 o+4.)
    Because is from the interval (0 o;90 o), the equation has two solutions: 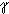1=15 o and 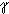2=75 o. While the first of them doesn't satisfy conditions stated in the problem specification, the second leads to the result a=60 o and ß=45 o.

  3. Let A=[0,0], B=[1,0], C=[c,d]. We are looking for such point M=[x,y] that the value of expression V(x,y)=|AM|2+|BM|2+|CM|2 be minimal. The distance of two points K=[x1,y1], L=[x2,y2] is d=sqrt((x1-x2)2+(y1-y2)2). Then
    V(x,y)=x2+y2+(1-x)2+y2+(x-c)2+(y-d)2
    which is equivalent to:
    V(x,y)=3x2-2x(c+1)+3y2-2yd+(1+c2+d2)

    Last member of the sum is constant and because x and y are independent, the expression V(x,y) is minimal when the contribution of members with x is minimal and at the same time the contribution of members with y is minimal. Therefore, we are looking for minimums of functions v1(x)=3x2-2x(c+1) and v2(y)=3y2-2yd. We rearrange the formulas:

    v1(x)=3[x2-(2/3x(c+1))]=3([x-(c+1)/3]2-((c+1)/9)2) =
    3(x-(c+1)/3)2-(c+1)2/3

    v2(y)=3(y2-(2yd)/3)=3[(y-d/3)2-d2/9]=3(y-d/3)2-d2/3
    The right member is constant and the left one is nonnegative in both expressions. That's why both expressions are minimal, when the left member is 0, so x=(c+1)/3 and y=d/3. Now we note that the centre of gravity of a triangle ABC has the coordinates
    T=[(0+1+c)/3,(0+0+d)/3]=[(c+1)/3,d/3]=[x,y]=M.

  4. Prove by contradiction: we suppose that each part was seen by at most two triangles. Take one triangle (A). He saw at most three parts which were seen by at most one more triangle. Therefore 5 triangles did not see any part together with A. One of them (B) saw (for the same reasons) a common part with at most three triangles from the remaining 4 and so there exists at least one triangle (C), which did not see a common part with A nor with B. No two triangles from the trio A, B, C saw a common part, which is our contradiction.

  5. Let M' is an image of point M in the central symmetry with the centre O. The following holds: OK is perpendicular to AB, OM' is perpendicular to BC. Because OK+OM+OL=zero_vector, we get ON' is parallel to KM' and M'K is perpendicular to CA. After rotating the triangle OM'K by -90 o, we can see that it is homothetic with the triangle ABC and thus there exists a real constant k, for which |OK|+|OM|+|ON|=k(a+b+c), where a=|BC|, b=|AC|, c=|AB| and k is a coefficient of homothety. It is enough to show that
    (|OK|+|OM|+|ON|)/(a+b+c)=k<=1/(2.sqrt(3))
    For an area of the triangle ABC, the following holds:
    SABC=SABO+SBCO+SACO=1/2.c.(k.c)+1/2.a.(k.a)+1/2.b.(k.b)=k/2(a2+b2+c2)
    from where
    k=(2SABC)/(a2+b2+c2).
    By the following arrangements using Heron's formula
    S=sqrt(s(s-a)(s-b)(s-c)), where s=(a+b+c)/2
    we get the inequality:
    (a2-b2)2+(a2-c2)2+(c2-b2)2>=0,
    a4+b4+c4+2a2b2+2b2c2+2c2a2>=3(-c4-a4-b4+2a2b2+a2c2+2a2b2)
    (a2+b2+c2)2/(4.3) >= 4 ( (a+b+c)(a+b-c)(a-b+c)(-a+b+c) )/16
    and using Heron's formula:
    (a2+b2+c2)/(2.sqrt(3)) >= 2SABC
    and thus the following really holds:
    1/(2.sqrt(3)) >= (2SABC)/(a2+b2+c2)=k.