z rovnosti n = x + y + u + v vyplyva xy
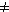 uv.
uv.
Skolsky rok 1998/99 - 3. seria zimnej casti
Prvocisla
1. Rieste rovnicu (n-4)2 = p3 + 9 , kde n je cele cislo a p je prvocislo.
2a. Dokazte, ze rovnica p2 + q2 = r2 + s2 + t2 , kde p,q,r,s,t su prvocisla, nema riesenie.
2b. Nech p a p2+2 su prvocisla. Dokazte, ze aj cislo p3+2 je prvocislo.
3a.
Dokazte, ze prirodzene cislo n (n>4) je prvocislom prave vtedy, ked
pre vsetky prirodzene cisla x,y,u,v
z rovnosti n = x + y + u + v vyplyva
xy 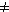 uv.
uv.
3b.
Postupnost {pn}n=1oo je rekurentne definovana takto:
p1 = 2 , a pre n
 N, n > 1 je pn najvacsi prvociselny
delitel cisla
p1. p2. p3. ... . pn-1+1.
Dokazte, ze ziadny clen tejto postupnosti nie je rovny 5.
N, n > 1 je pn najvacsi prvociselny
delitel cisla
p1. p2. p3. ... . pn-1+1.
Dokazte, ze ziadny clen tejto postupnosti nie je rovny 5.
4a. Dokazte, ze ak p je prvocislo, tak cislo

|
|

|
4b.
Dokazte, ze ak p je prvocislo a n je prirodzene cislo (n
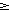 p), tak
cislo
p), tak
cislo

|
|

|
- |
|
|
|
5a. Dokazte, ze ku kazdemu prvocislu p existuju cele cisla u,v take, ze p|1+u2+v2.
5b.
Zlomok q/p, kde p 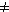 5 je neparne prvocislo, je
napisany v desatinnom (periodickom) tvare. Dokazte, ze pocet
cislic v (najmensej) periode je parny prave vtedy, ked ich aritmeticky
priemer je rovny 9/2.
5 je neparne prvocislo, je
napisany v desatinnom (periodickom) tvare. Dokazte, ze pocet
cislic v (najmensej) periode je parny prave vtedy, ked ich aritmeticky
priemer je rovny 9/2.
Priklady tejto serie vybrali Eno Kovac (1, 2b, 3a, 4a, 5a), Juraj Foldes (3b, 4b, 5b) a Jan Spakula (2a).