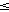 2n . Dokazte, ze pre lubovolne
prirodzene cislo n existuju jej cleny ap, aq take, ze
ap - aq = n .
2n . Dokazte, ze pre lubovolne
prirodzene cislo n existuju jej cleny ap, aq take, ze
ap - aq = n .
Skolsky rok 1998/99 - 1. seria letnej casti
Konecno a Nekonecno
1. Pre prirodzene cislo n nech G(n) znamena jeho ciferny sucet (ak je zapisane v desiatkovej sustave). Dokazte, ze pre kazde prirodzene cislo n je nekonecna postupnost G(n), G(G(n)), G(G(G(n))), ... od nejakeho clena konstantna. Najdite tuto konstantu pre n=19992000.
2a. Na priamke je danych konecne vela (aspon pat) bodov. Kazdy z nich je zafarbeny jednou zo styroch farieb, pricom kazdou farbou je zafarbeny aspon jeden bod. Dokazte, ze na tej priamke existuje usecka, ktora obsahuje po prave jednom bode z nejakych dvoch farieb a po aspon jednom bode zo zvysnych dvoch farieb.
2b.
Nekonecna postupnost prirodzenych cisel a1 < a2 < a3 < ...
splna podmienky a1=1 , an+1 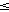 2n . Dokazte, ze pre lubovolne
prirodzene cislo n existuju jej cleny ap, aq take, ze
ap - aq = n .
2n . Dokazte, ze pre lubovolne
prirodzene cislo n existuju jej cleny ap, aq take, ze
ap - aq = n .
3a.
Nech n je prirodzene cislo nesudelitelne s cislami 2 a 5. Dokazte, ze
potom sa v desatinnom zapise cisla 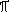 nachadza taky usek, ktory
je delitelny n (tento usek berieme ako nejake prirodzene cislo;
napr. prve tri cifry za desatinnou ciarkou nam daju cislo 141).
nachadza taky usek, ktory
je delitelny n (tento usek berieme ako nejake prirodzene cislo;
napr. prve tri cifry za desatinnou ciarkou nam daju cislo 141).
3b.
Na konecnej mnozine S je dana operacia * (t.j. pre lubovolne
a,b  S je a*b
S je a*b  S),
ktora je asociativna (t.j.
(a*b)*c = a*(b*c) pre lubovolne a,b,c
S),
ktora je asociativna (t.j.
(a*b)*c = a*(b*c) pre lubovolne a,b,c  S).
S).
a) Dokazte, ze S obsahuje prvok u taky, ze u*u=u.
b) Najdite priklad nekonecnej mnoziny S, v ktorej taky
prvok neexistuje.
4a. Najdite vsetky konecne postupnosti (c0, c1, c2, ... , cn ) nezapornych celych cisel take, ze pre kazde i=0,1,2, ... ,n sa cislo i nachadza v tejto postupnosti nachadza prave ci-krat a nenachadzaju sa v nej ziadne ine cisla.
4b. Dokazte, ze neexistuje nekonecna postupnost x1, x2, x3, ... taka, ze pre lubovolne prirodzene cisla n,p,q plati

5a.
Dokazte, ze existuje len konecny pocet prirodzenych cisel n takych,
ze n je delitelne vsetkymi prirodzneymi cislami, ktore su mensie
alebo rovne ako 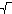 n a najdite tieto cisla.
n a najdite tieto cisla.
5b. Dany je konecny pocet prirodzneych cisel, z ktorych kazde je mensie ako 1000, ale najmensi spolocny nasobok lubovolnych dvoch je vacsi ako 1000. Dokazte, ze sucet prevratenych hodnot tychto cisel je mensi ako 2.
L.C.Larson: Metody riesenia matematickych problemov}
Priklady tejto serie vybrali Eno Kovac (1, 2a, 2b, 3b, 4a), Feldo Foldes (3a, 5a, 5b) a Jano Babela (4b).