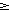1. V rovine je dany konecny pocet bodov, z ktorych ziadne tri nelezia na jednej priamke. Niektore dvojice bodov su spojene useckami tak, ze z kazdeho bodu vychadzaju najviac tri usecky. Dokazte, ze tieto body mozme ofarbit dvoma farbami tak, aby bol kazdy bod spojeny useckou s najviac jednym bodom tej istej farby (ako ma on sam).

2a. Urcte maximalny pocet konov, ktore mozno umiestnit na sachovnicu 8×8 tak, aby sa ziadne dva neohrozovali.

2b. Dane je prvocislo p>2 a prirodzene cislo n. Kolkymi sposobmi mozno ofarbit vrcholy pravidelneho p-uholnika pomocou n farieb? Dve ofarbenia pokladame za rozne ak nemozno z jedneho dostat druhe otocenim mnohouholnika.

3a. Urcte kolkymi sposobmi mozeme vypocitat sucin x₁·x₂·...·x_n (kde n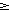2 je prirodzene cislo), ak vieme nasobit naraz len dve cisla a mozeme lubovolne menit poradie cinitelov.

3b. Mame n urien, v ktorych su zlte a modre listky. Pre k=1,2,...,n je v k-tej urne 3k zltych a 5k modrych listkov. Z prvej urny vyberieme nahodne jeden listok a vlozime ho do druhej urny. Potom vyberieme listok z druhej urny a vlozime ho do tretej. Takto pokracujeme, az vyberieme listok z n-tej urny a vlozime ho do prvej. Potom vyberieme z prvej urny jeden listok. Aka je pravdepodobnost, ze bude zlty?

4a. Mnozina X ma 1999 prvkov. Nech S₁,S₂,...,S_m je system jej podmnozin, ktory splna nasledujuce podmienky:

(i)Zjednotenim ktorejkolvek trojice tychto mnozin je cela mnozina X.

(ii)Zjednotenie lubovolnych dvoch z tychto mnozin ma nanajvys 1996 prvkov.

4b. Na stole je n knih ulozenych v niekolkych kopkach. Knihovnik ich kazdy den prerovna tak, ze z kazdej kopky odoberie jednu knihu a z nich potom vytvori dalsiu kopku. Pritom si do zosita pise pocty knih v jednotlivych kopkach (zoradene podla velkosti). Potom:

a) Po nejakom case sa zacnu zapisy pravidelne opakovat. Dokazte!

b) Ak po nejakom case budu zapisy kazdy den rovnake, tak

n =		k
		2

pre vhodne prirodzene cislo k. Dokazte.

c) Plati tvrdenie b) aj obratene?

5a. V jednom meste niekolko ludi nachladlo, a tak vypukla chripkova epidemia (v nasledujucich dnoch uz nikto nenachladol a chripka sa sirila kvapockovou nakozou). Choroba vypukne druhy den po nakaze (vtedy je clovek infekcny) a trva vzdy jeden den. Dalsi den je clovek imunny (na jeden den) a potom je uz zdravy (a moze sa zase nakazit). Pritom kazdy zdravy obcan navstivi kazdy den vsetkych svojich chorych priatelov a pri tej prilezitosti sa od nich nakazi. Dokazte, ze ak nebol prvy den nikto imunny, tak epidemia jedneho krasneho dna skonci. Ostane toto tvrdenie v platnosti ak pripustime, ze prvy den epidemie bol niekto vdaka ockovaniu imunny?

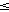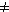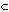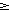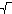5b. Nech X je n-prvkova mnozina a  A₁,A₂,...,A_n su jej trojprvkove podmnoziny take, ze |A_iA_j|1 pre ij. Dokazte, ze existuje mnozina AX taka, ze ziadna z mnozin A₁,A₂,...,A_n nie je podmnozinou mnoziny A a plati |A| [(2n)] (pricom [x] oznacuje dolnu celu cast realneho cisla x).

J.Sedlacek: Faktorialy a kombinacni cisla, SMM 10
A.Vrba: Princip matematicke indukce, SMM 40
A.Vrba: Kombinatorika, SMM 45
A.Plocki: O nahode a pravdepodobnosti, SMM 50

Priklady tejto serie vybrali Eugen Kovac (3a, 3b, 5b) a Juraj Foldes (1, 2a, 2b, 4a, 4b, 5a).