Kruznice v mnohouholniku 2

1.V obore realnych cisel rieste system rovnic

x1(x1 - 1) = x2 - 1,    x2(x2 - 1) = x3 - 1,     ...    xn(xn - 1) = x1 - 1.

2a.Dokazte, ze ak funkcia f: R -> R vyhovuje pre vsetkyx,y Rnerovnostiam

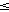f(x) x, f(x + y) 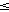f(x) + f(y),
tak pre kazde x R plati f(x) = x.

2b.Najdite vsetky funkcie f : R -> R splnajuce pre vsetkyx R rovnicu

xf(x) + f(1-x) = x3 - x .

3a.Vnutri trojuholnika ABC lezi bod O. Dokazte, ze plati nerovnost (pri standartnom oznaceni)

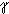|OA| cos a/2 + |OB| cos ß/2} + |OC| cos /gamma/2 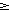(a+b+c)/2.

3b.Nech a,x,y,z su realne cisla, pre ktore plati

(cos x + cos y + cos z)/cos(x + y + z)= (sin x + sin y + sin z)/sin(x + y + z) = a .
Dokazte, ze potom
cos(x+y) + cos(z+x) + cos(y+z) = a .

4a.Polynom stupna n N vyhovuje rovnostiam P(k)=k/(k+1) pre k = 0,1,...,n. Urcte P(n+1).

4b.Nech f1, f2, f3,... je { Fibonacciho postupnost}(t.j. f1 = f2 = 1 a  fn+2 = fn+1 + fn pre n N). Ak pre polynom P(x) stupna 998 plati P(k) = fk pre k = 1000, 1001,..., 1998 , potomP(1999) = f1999 - 1. Dokazte.

5a.Dokazte, ze pre kazde n N plati
2n
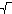n
.3n < 4n.

5b.Pre pevne n N najdite najmensiu moznu hodnotu vyrazu

x1 + (x22)/2 + (x33)/3 + ... + (xnn)/n .
ak x1,x2,...,xn su kladne realne cisla, pre ktore plati
1/x1 + 1/x2 + ... + 1/xn = n .

Priklady tejto serie vybrali Feldo Foldes (1, 2b, 3b, 5a, 5b), Eno Kovac (2a, 2b, 3a, 4a, 4b), Vlado Marko (2b) a Slavo Spakula (4a).

Odporucena literatura

L.C. Larson: Metody riesenia matematickych problemov
J. Sedivy: Shodna zobrazeni v konstruktivnich ulohach, SMM 3
M. Sisler, J. Jarnik: O funkcich, SMM 4
J. Hornik: Ulohy o maximech a minimech funcki, SMM 17
B. Budinsky, S. Smakal: Goniometricke funkce, SMM 20