Zadanie:
Kúzelníci Miťo a Mazo si pripravili malé vystúpenie. Na začiatku
je v miestnosti
s divákmi len Mazo. Diváci uložia  mincí do ľubovoľnej postupnosti znakov a
hláv a vyberú si jedno číslo z množiny mincí do ľubovoľnej postupnosti znakov a
hláv a vyberú si jedno číslo z množiny  . Mazo potom otočí práve
jednu mincu naopak a zavolá Miťa zo zákulisia, ktorý sa z
rozloženia mincí snaží
uhádnuť, aké číslo si diváci vybrali. . Mazo potom otočí práve
jednu mincu naopak a zavolá Miťa zo zákulisia, ktorý sa z
rozloženia mincí snaží
uhádnuť, aké číslo si diváci vybrali.
a) Dokážte, že ak sa toto kúzlo dá spraviť pre 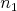 a a 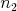 , potom sa dá
spraviť aj pre , potom sa dá
spraviť aj pre 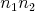 . .
b) Nájdite všetky  , pre ktoré sa toto kúzlo dá spraviť. , pre ktoré sa toto kúzlo dá spraviť. |



