|
|
 |
8. príklad 2. letnej série 2008/2009
Zadanie:
Drak má v jaskyni zaujímavú dvojicu trojuholníkov. Platí pre ne,
že dve strany jedného trojuholníka sú rovnako dlhé ako niektoré
dve strany druhého trojuholníka a že trojuholníky sú podobné
(ale nie nutne zhodné). Drak hrdo vyslovil nasledujúce tvrdenie:
Keby som mal hocijakú dvojicu trojuholníkov s takýmito
vlastnosťami, tak koeficient podobnosti týchto trojuholníkov by
bolo číslo medzi 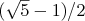 a a  a nebolo by rovné týmto krajným hodnotám. Dokážte, že drak
má pravdu. a nebolo by rovné týmto krajným hodnotám. Dokážte, že drak
má pravdu. |
peťo <peto~kms~sk> - 16. 04. 2009 - 22:39:36 z 158.195.165.27HAgO napísal:
to
mas z toho ze nie si kapusta ta ma aspon
hlavu... |
veru veru, drak ma hlavy tri, takze mu nerobi problem povedat TAKU
vetu :).
cituj ma |
| HAgO - 09. 04. 2009 - 22:20:34 z chello085216147110.chello.skto mas z toho ze nie si kapusta ta ma aspon hlavu... cituj ma |
| Petrzlen - 08. 04. 2009 - 19:55:30 z adsl-dyn131.78-99-81.t-com.skKrasne zadanie (hlavne pasaz drak hrdo vyslovil:"), zabralo mi,
kym som mu pochopil. Myslim, ze tento priklad mal najvyssi pomer:
(obtiaznost zadania) / (obtiaznost riesenia) cituj ma |
|
|
 |
|
|



