|
|
 |
4. príklad 1. letnej série 2008/2009
Zadanie:
Napíšme si čísla  v ľubovoľnom poradí, každé práve raz. Prvé z nich označme v ľubovoľnom poradí, každé práve raz. Prvé z nich označme 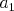 , druhé , druhé 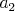 a takto postupne až po posledné, ktoré označíme a takto postupne až po posledné, ktoré označíme 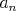 . Dokážte, že ak . Dokážte, že ak  je nepárne, tak potom súčin je nepárne, tak potom súčin 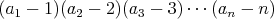 je párne číslo. je párne číslo. |
Zuska - 11. 03. 2009 - 22:16:38 z 158.195.165.26To aby sa zvyraznila kolisajuca situacia na trhu s prirodzenymi
cislami. cituj ma |
| Ondráč - 10. 03. 2009 - 22:19:55 z pupendo.ubyt.sdjls.uniba.skTie vlnovky tam vyzerajú štýlovo :) cituj ma |
| zuska & katka - 06. 03. 2009 - 11:20:44 z 158.195.165.26Este raz!
Našim cieľom je dokázať, že súčin 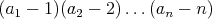 je párny. To platí vtedy, keď je aspoň jedna zátvorka párna. A
kedy platí toto? Rozdiel dvoch čísel je párny vtedy, keď je ich
parita rovnaká, teda obe musia byť párne alebo obe nepárne.
Podobne, rozdiel dvoch čísel je nepárny vtedy, keď je ich parita
rôzna. Musíme teda dokázať, že pre každé nepárne je párny. To platí vtedy, keď je aspoň jedna zátvorka párna. A
kedy platí toto? Rozdiel dvoch čísel je párny vtedy, keď je ich
parita rovnaká, teda obe musia byť párne alebo obe nepárne.
Podobne, rozdiel dvoch čísel je nepárny vtedy, keď je ich parita
rôzna. Musíme teda dokázať, že pre každé nepárne  musí byť medzi našimi zátvorkami aspoň jedna párna. A~prečo by
to malo platiť? musí byť medzi našimi zátvorkami aspoň jedna párna. A~prečo by
to malo platiť?
Všimnime si, že pre nepárne  platí, že nepárnych čísel je od 1 po platí, že nepárnych čísel je od 1 po  o jedno viac, než párnych. Nepárnych je presne o jedno viac, než párnych. Nepárnych je presne 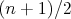 a párnych a párnych 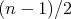 . Teraz sa na celú úlohu môžeme pozrieť napríklad týmito dvoma
spôsobmi: . Teraz sa na celú úlohu môžeme pozrieť napríklad týmito dvoma
spôsobmi:
a) Ak je medzi číslami  o~jedno viac nepárnych čísel ako párnych, potom to isté platí
pre čísla o~jedno viac nepárnych čísel ako párnych, potom to isté platí
pre čísla 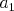 až až 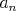 . Teraz poďme ukázať, že súčin . Teraz poďme ukázať, že súčin 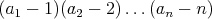 nikdy nemôže byť nepárny (teda sa pokúsime o~dôkaz sporom). Ak
by tento súčin mal byť nepárny, potom každá zo zátvoriek musí
byť nepárna. To znamená, že do zátvoriek budeme zatvárať
dvojice párny - nepárny. Vieme, že párnych čísel je o jedno
menej ako nepárnych aj medzi nikdy nemôže byť nepárny (teda sa pokúsime o~dôkaz sporom). Ak
by tento súčin mal byť nepárny, potom každá zo zátvoriek musí
byť nepárna. To znamená, že do zátvoriek budeme zatvárať
dvojice párny - nepárny. Vieme, že párnych čísel je o jedno
menej ako nepárnych aj medzi  až až  , aj medzi , aj medzi 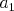 až až 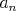 . Preto, keď budeme vytvárať dvojice párny - nepárny, zostane
nám nakoniec po jednom nepárnom čísle z~oboch skupín, a~tie
musíme zavrieť do zátvorky spolu. Ich rozdiel bude párne číslo,
a preto aj celkový súčin . Preto, keď budeme vytvárať dvojice párny - nepárny, zostane
nám nakoniec po jednom nepárnom čísle z~oboch skupín, a~tie
musíme zavrieť do zátvorky spolu. Ich rozdiel bude párne číslo,
a preto aj celkový súčin 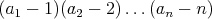 ~bude párny. ~bude párny.
b) (podľa Mariána Horňáka) Zasa využijeme, že medzi  až až  aj medzi aj medzi 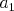 až až 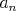 je nepárnych čísel o~jedno viac, než párnych. Keďže je ich
v~každej skupine je nepárnych čísel o~jedno viac, než párnych. Keďže je ich
v~každej skupine 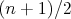 a~každé číslo použijeme v~zátvorkách dvakrát, potom máme a~každé číslo použijeme v~zátvorkách dvakrát, potom máme  nepárnych čísel, ktoré chceme dať do nepárnych čísel, ktoré chceme dať do  zátvoriek. No a~z~toho vidíme, že v aspoň jednej zátvorke musia
byť spolu dve nepárne čísla (takáto úvaha sa podľa jedného
múdreho uja volá Dirichletov pricíp), ktorých rozdiel je párne
číslo, čo sme chceli dokázať. zátvoriek. No a~z~toho vidíme, že v aspoň jednej zátvorke musia
byť spolu dve nepárne čísla (takáto úvaha sa podľa jedného
múdreho uja volá Dirichletov pricíp), ktorých rozdiel je párne
číslo, čo sme chceli dokázať.
\end{enumerate}
Komentár: Väčšina z~vás s~úlohou nemala problémy. Treba si
však dať pozor na to, že ak niečo dokážem napríklad pre  , ešte to neznamená, že to platí všeobecne. , ešte to neznamená, že to platí všeobecne. cituj ma |
|
|
 |
|
|



