|
|
 |
5. príklad 2. letnej série 2007/2008
Zadanie:
Nech 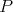 je bod vnútri trojuholníka je bod vnútri trojuholníka 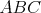 . Zostrojme úsečky rovnobežné so stranami trojuholníka
prechádzajúce bodom . Zostrojme úsečky rovnobežné so stranami trojuholníka
prechádzajúce bodom 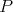 . Obsahy troch trojuholníkov, ktoré nám týmto vznikli, sú . Obsahy troch trojuholníkov, ktoré nám týmto vznikli, sú 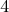 , , 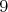 a a 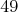 . Aký je obsah trojuholníka . Aký je obsah trojuholníka 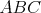 ? ? |
JllpR2sw <kmdh1pqm3j~gmail~com> - 03. 03. 2014 - 15:36:16 z 108.63.29.19QuotesChimp is utterly essential that you simply recognize what's
leave off beneath your insurance contract. If Not, you may find
yourself using a reduction that you wrongly presumed there turned out
to be treatment inside the coverage. cituj ma |
| USmwB48F <berndolaf1962~web~de> - 06. 11. 2013 - 06:09:34 z 188.143.232.12Rori, tfdch diagramov je naaozj len niekoľko, ak izomorfne9 diagramy
považujeme za jeden a ten istfd diagram (t.j. dva diagramy
považujeme za rovnake9 ak sa ledšia len očedslovanedm vrcholov a
predpadne vfdmenou farieb.) Pre predpad, že každfd vrchol je
spojenfd s každfdm nejakou orientovanou cestou, neme1me ne1sobne9
hrany ani slučky a z každe9ho vrchola vyche1dza pre1ve jedna
červene1 a pre1ve jedna čierna hrana, tak som našiel iba dva
take9to grafy. Z grafu uvedene9ho na obre1zku je možne9 spraviť ten
druhfd tak, že modrfd cyklus dĺžky 3 opačne orientujeme. Ale ak by
si chcel ne1jsť nejakfd zaujedmavfd diagram, tak nemusedš
preche1dzať systematicky všetkfdmi diagramami. Stačed ne1hodne
vygenerovať pe1r tisedcok (povedzme, že pripustedš aj slučky, ale
nie ne1sobne9 hrany) a z nich vyberieš ten najzaujedmavejšed
(napredklad s najdlhšedm optime1lnym riešenedm). Ak je tfdch tried
neizomornfdch grafov me1lo, tak s veľkou pravdepodobnosťou
natrafedš aspoň na jedne9ho reprezentanta tejto triedy. Inak to
Tvoje riešenie Černe9ho diagramu je spre1vne. (Program, alebo si to
tak rfdchlo uvidel se1m? :-) cituj ma |
| misof - 08. 04. 2008 - 13:10:58 z foja.dcs.fmph.uniba.skAha hej, ono sa to fakt dá nasekať až na 144 maličkých
trojuholníkov s plochou 1 :)
Inak teda aj to moje riešenie využíva ten fakt čo spomínaš, že
obsah rastie s druhou a objem s treťou mocninou strany. Takýto
pohľad je podľa mňa celkom užitočné mať
"vžité".
Ako tá klasická úloha s maslom: Janko si kúpil maslo. Potom, ako
si ním týždeň natieral chleby, sa rozmery masla zmenšili na
polovicu. Koľko dní mu ešte maslo vydrží? cituj ma |
| |
| |
| ika - 06. 04. 2008 - 11:38:12 z 158.195.160.93Inak ten priklad sa dal strasne krasne vyriesit, ale zatial som
nenadabyla na nikoho co to tak riesil, a to uz mam temer vsetko
pozrete.
Fakt sa to dalo uplne super riesit bez ratania pomerou a kdeakych
inych nechutnosti. cituj ma |
| ika - 06. 04. 2008 - 11:35:50 z 158.195.160.93ej nejak mrtvo tu je cituj ma |
|
|
 |
|
|



