Zadanie:
Nech 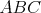 je trojuholník s opísanou kružnicou je trojuholník s opísanou kružnicou  . Kružnica . Kružnica 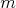 leží vnútri uhla leží vnútri uhla 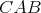 , dotýka sa strán , dotýka sa strán
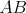 , , 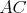 v bodoch v bodoch 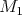 , , 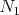 a dotýka sa vnútra kružnice a dotýka sa vnútra kružnice  v bode v bode 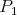 .
Body .
Body 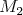 , , 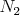 , , 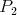 a a 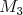 , , 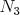 , , 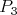 sú definované podobne pre uhly sú definované podobne pre uhly 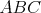 a a 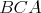 .
Ukážte, že úsečky .
Ukážte, že úsečky 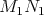 , , 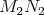 a a  sa pretínajú v jednom bode, ktorý je zároveň ich spoločným
stredom. sa pretínajú v jednom bode, ktorý je zároveň ich spoločným
stredom. |



