kms - fórum o príkladoch

10. príklad 2. zimnej série 2008/2009

Zadanie:
Nájdite všetky prvočísla $p$ , pre ktoré existujú kladné celé čísla $n$ , $x$ , $y$ spĺňajúce rovnosť

$p^n=x^3+y^3.$

UZ1T1m9n4YdS <dbh6zc3q3xe~yahoo~com> - 27. 06. 2014 - 01:14:21 z ec2-54-86-11-67.compute-1.amazonaws.com

Ahoj Moni, čedm začedt, asi ne1hrdelnedkem, ten se mi moc ledbed.Do deky z africkfdch květů ti přeji hodně trpělivosti a rdsoat Makeefa je kouzelne1, je vidět, že vedš, co se mu ledbed.Měj se pěkně IVA

cituj ma

8adOAEpsauq3 <buelnpiw10n~mail~com> - 26. 06. 2014 - 22:55:05 z 62-210-78-179.rev.poneytelecom.eu

... ஒர ட ய ம ப ஸ க ட ட ய ம எட த த வச ச க க ட ட ம ன ன ற ப ட த த ன பட க கவ ஆரம ப ச ச ன உங க பத வ . ப த ல பச ச சத ன ன ஃப ள வ ட ட ப ப ய ட ம ல. இந தத த ற ஒர unorganised secotr. எப பட ப ப ர த த ல ம தட எட த தவன த ன தண டல க ரன என ற ந லம த ன . ய ன யன இல ல ன ன அத க த தட ம வ ல ய க ப ப ய வ ட ம . spb ஒர ச ன னத த ர ந கழ ச ச ய ல ச ன ன ர ; ச ன வ சன என பவர ம யற ச ய ல த ன எல ல ய ன யன ஓக . த ழ ல ள சம பளம வந த ட ச ச ன ன ச ன ன த த ன ப ர ன ட ல ப ல இர ந த ப க ம ங க ற ந லம ய க க ண ட ந த ர . அதன ல த ன ப ட னத ம க ச க ட க க ற ங க என ற .அப பட ச ய ததற க க ச ன வ சன பட தப ட பட ட ர க க ர பட ம தல ள கள க ட ட என ற .]]]உண ம த ன . உண ம ய ன கம ய ன ஸவ த த ர .எம .ப .ச ன வ சன .. வ ழ க..! அவர ல த ன இன ற க க த ர ய லகம இன ற க க ம கப ப ர ய வ ய ப ர க ந த ரம க வளர ந த ர க க றத என ற ச ல லல ம ..!

cituj ma

2grnB7Axde <8ou9vgff3~gmail~com> - 26. 06. 2014 - 11:12:00 z 62-210-78-179.rev.poneytelecom.eu

Tak je1 si tipnu :-) Buď to bude nějake1 pare1dned kabelka, barvy jsou opvardu kre1sne9!!! Nebo přehoz?A velryba... je1 si myslela, že je to nějakfd ve1leced polšte1řek a teď videdm, že je to takove1 muchlovaced hračka :-) Ale rozhodně mě to neodradilo od ušited jedne9 pro našeho marňouse :-) Jola

cituj ma

Lenika <lenka~bendova~gmail~com> - 15. 11. 2008 - 21:17:03 z adsl-dyn165.78-99-234.t-com.sk

No hej - to si necakal moje meno pri takom vysokom cisle prikladu;)

no apsom ze tak, uz som si skoro zacala mysliet ze som uplne mimo=)
teda trosku som aj tak ale nie uplne;)

cituj ma

bus - 13. 11. 2008 - 12:19:17 z dsl-static-251.213-160-168.telecom.sk

2 a 3 Lenika ;). A jej ty si poslala aj moj priklad :).

cituj ma

myrec - 12. 11. 2008 - 22:20:04 z 158.195.173.98

no znamena to ze pre p<>3 je to len p=2 a pre p=3 kazdy kto sa pokusal nasiel riesenie :P

cituj ma

Lenika <lenka~bendova~gmail~com> - 12. 11. 2008 - 21:51:40 z ip-195-098-027-247.static.nextra.sk

Dufam ze tym nechces povedat ze sa to da len pre p=2?

cituj ma

bus - 12. 11. 2008 - 17:11:02 z dsl-static-251.213-160-168.telecom.sk

Tak mna si presvedcil :).

cituj ma

misko sz - 11. 11. 2008 - 23:03:44 z misko.kolej.mff.cuni.cz

Znie to celkom doveryhodne, nie?

cituj ma

misko sz - 11. 11. 2008 - 23:03:17 z misko.kolej.mff.cuni.cz

Uvazujem:

$x^3+y^3 = (x+y)(x^2-xy+y^2)$

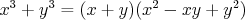
To ma byt nejake prvocislo. Pacilo by sa mi, ak by boli tie zatvorky nesudelitelne. Su? Spocitam NSD:

$(x+y, x^2-xy+y^2) = (x+y,3y^2)$

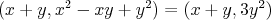
Ak p=3, najdeme riesenie 3^2 = 2^3+1^3. Teda odteraz p <> 3. Teda NSD nemoze byt 3:

$\cdots = (x+y,y^2)$

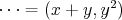
BUNV x a y su nesudelitelne (riesenia, kde su sudelitelne viem redukovat na riesenia, kde sudelitelne nie su, mozno az na par pripadov, co ide rucne rozobrat). Potom zrejme ziadne prvocislo deliace y^2 nedeli x+y, takze

$NSD(x+y, x^2-xy+y^2) = 1$

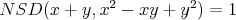
Hura, z toho vyplyva

$x+y = 1 \quad \text{alebo} \quad x^2-xy+y^2 = 1$

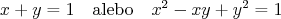
Prva moznost neprichadza do uvahy kedze x,y su prirodzene, druha odpadne z odhadu

$x^2-xy+y^2 = (x-y)^2 + xy \geq 1$

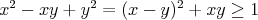
Roznost nastava prave vtedy, ked x=y, z coho dostanem riesenie pre p=2. A to uz vyzera, ze to je vsetko :)

cituj ma