|
|
 |
10. príklad 2. letnej série 2007/2008
Zadanie:
Rozhodnite, či existuje funkcia 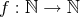 taká, že pre všetky taká, že pre všetky 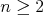 platí platí
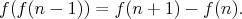
|
|
| Tomas Ko. <tomas~kocak~gmail~com> - 09. 04. 2008 - 20:04:56 z nat-88-212-22-164.antik.sktak ale ja som urcite takuto chybu neurobil a som fakt skutocne
zvedavy preco som tam stratil dva body... :) ako neviem si predstavit
co som tam zanedbal alebo neobkecal alebo co tam mam vlastne zle cituj ma |
| |
| škrečok - 31. 03. 2008 - 18:07:54 z 158.195.162.145naozaj sa to nedalo ;) cituj ma |
| Kubo - 30. 03. 2008 - 10:35:08 z adsl-dyn247.91-127-207.t-com.skDufam ze sa to naozaj nedalo... cituj ma |
|
|
 |
|
|



