|
|
 |
8. príklad 3. zimnej série 2008/2009
Zadanie:
Na zabudnutej tabuli v Rasťovej ešte zabudnutejšej tmavej komnate
je nakreslených päť už skoro zabudnutých úsečiek. Z každej
trojice z týchto úsečiek vieme zložiť trojuholník. Dokážte,
že vieme vybrať tri úsečky tak, že trojuholník, ktorý z nich
vznikne, je ostrouhlý (na také sa nezabúda). |
viktor.sz - 07. 12. 2008 - 12:57:03 z adsl-dyn149.78-99-172.t-com.skjj mam to nejak tak len o trochu viac rozpisane ale postup je rovnaky
:-) cituj ma |
| skiller - 06. 12. 2008 - 14:39:59 z localhostmišof napísal:
No neviem nakoľko bude toto elegantné, ale budiž:
Označme si dĺžky úsečiek 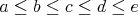 . Ak majú všetky trojuholníky existovať, musí platiť . Ak majú všetky trojuholníky existovať, musí platiť 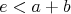 . .
Trojuholník so stranami 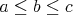 je ostrouhlý práve vtedy, keď je ostrouhlý práve vtedy, keď 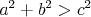 (lebo kosínusová veta, čo je len väčší brat Pytagorovej). (lebo kosínusová veta, čo je len väčší brat Pytagorovej).
Ak by teda nebol žiaden trojuholník ostrouhlý, tak pre strany 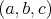 , , 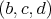 a a 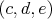 dostávame dostávame 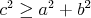 , , 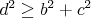 a a 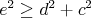 . Dosadením prvých dvoch nerovností do tretej dostávame, že musí
platiť . Dosadením prvých dvoch nerovností do tretej dostávame, že musí
platiť 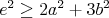 . .
Ale 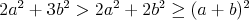 , čo je spor s , čo je spor s 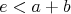 . Čím sme dokonca dokázali, že aspoň jeden z nami zvolených
troch trojuholníkov musí byť ostrouhlý. . Čím sme dokonca dokázali, že aspoň jeden z nami zvolených
troch trojuholníkov musí byť ostrouhlý. |
cituj ma |
| mišof - 06. 12. 2008 - 02:21:58 z adsl-dyn116.78-99-158.t-com.skNo neviem nakoľko bude toto elegantné, ale budiž:
Označme si dĺžky úsečiek 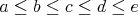 . Ak majú všetky trojuholníky existovať, musí platiť . Ak majú všetky trojuholníky existovať, musí platiť 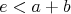 . .
Trojuholník so stranami 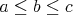 je ostrouhlý práve vtedy, keď je ostrouhlý práve vtedy, keď 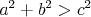 (lebo kosínusová veta, čo je len väčší brat Pytagorovej). (lebo kosínusová veta, čo je len väčší brat Pytagorovej).
Ak by teda nebol žiaden trojuholník ostrouhlý, tak pre strany 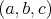 , , 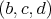 a a 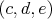 dostávame dostávame 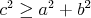 , , 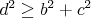 a a 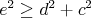 . Dosadením prvých dvoch nerovností do tretej dostávame, že musí
platiť . Dosadením prvých dvoch nerovností do tretej dostávame, že musí
platiť 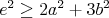 . .
Ale 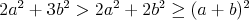 , čo je spor s , čo je spor s 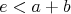 . Čím sme dokonca dokázali, že aspoň jeden z nami zvolených
troch trojuholníkov musí byť ostrouhlý. . Čím sme dokonca dokázali, že aspoň jeden z nami zvolených
troch trojuholníkov musí byť ostrouhlý. cituj ma |
| tina - 04. 12. 2008 - 20:04:47 z bip-static-13.213-81-131.telecom.skhm...ja som to riešila sporom....dúfam, že dobre... cituj ma |
| kamilama - 03. 12. 2008 - 21:44:58 z 158.196.244.87.in-addr.arpanajde sa nejaky dobrak a ukaze mi na tento priklad krasne elegantne a
fintove riesenie? neverim ze take nie je a ze sa to nedalo inak ako
tak hnusne cituj ma |
|
|
 |
|
|



