|
|
 |
10. príklad 1. zimnej série 2009/2010
Zadanie:
Doma u Chucka na stole je  rôznych na sebe položených kníh. Knihy začal nasledovne
otáčať. V prvom ťahu otočil najvrchnejšiu knihu a položil ju
naspäť. V druhom ťahu otočil dve vrchné knihy ako jeden blok a
položil ich naspäť. Takto pokračoval aj ďalej a v rôznych na sebe položených kníh. Knihy začal nasledovne
otáčať. V prvom ťahu otočil najvrchnejšiu knihu a položil ju
naspäť. V druhom ťahu otočil dve vrchné knihy ako jeden blok a
položil ich naspäť. Takto pokračoval aj ďalej a v  -tom ťahu otočil všetkých -tom ťahu otočil všetkých  kníh ako jeden blok a položil ich naspäť. V kníh ako jeden blok a položil ich naspäť. V  -vom ťahu otočil opäť vrchnú knihu a položil ju naspäť. V -vom ťahu otočil opäť vrchnú knihu a položil ju naspäť. V  -hom ťahu otočil vrchné dve knihy ako jeden blok a položil ich
naspäť. Takýmto spôsobom otáčal aj ďalej. Chuck odmieta
skončiť skôr než sú knihy uložené presne tak, ako na
začiatku, teda nielen v správnom poradí, ale aj správne
orientované.
Orientáciu knihy rozlišujeme podľa toho, či je kniha otočená
prednou
obálkou nahor alebo nadol. Všimnite si, že pri otočení nejakého
bloku
kníh sa orientácia každej knihy tohoto bloku zmení. Dokážte, že
Chuck po konečnom počte ťahov skončí. -hom ťahu otočil vrchné dve knihy ako jeden blok a položil ich
naspäť. Takýmto spôsobom otáčal aj ďalej. Chuck odmieta
skončiť skôr než sú knihy uložené presne tak, ako na
začiatku, teda nielen v správnom poradí, ale aj správne
orientované.
Orientáciu knihy rozlišujeme podľa toho, či je kniha otočená
prednou
obálkou nahor alebo nadol. Všimnite si, že pri otočení nejakého
bloku
kníh sa orientácia každej knihy tohoto bloku zmení. Dokážte, že
Chuck po konečnom počte ťahov skončí. |
mišof - 12. 10. 2009 - 17:27:35 z dial-95-105-152-199-orange.orange.skNena: Podrobne:
Krok 1: Predstav si, že vyrábaš ľubovoľnú nekonečnú
postupnosť vecí (vec1, vec2, vec3, atď.), kde z každého člena
vieš jednoznačne určiť nasledujúci. Akonáhle sa ti stane, že
vyrobíš vec, ktorú si vyrobila už predtým, postupnosť, ktorú
vyrábaš, sa nutne zacyklila -- lebo odteraz budeš nutne opakovať
dokola presne to, čo si robila, odkedy si túto vec vyrobila
prvýkrát.
Príklad: Počítaš 1 deleno 110. Postupnosť, ktorú vyrábaš, sú
aktuálne zvyšky počas delenia. Nový zvyšok je jednoznačne
určený predchádzajúcim: zoberieš aktuálny zvyšok, pripíšeš
nulu (t.j. vynásobíš ho 10), dostaneš X. Celá časť X/110 je
ďalšia cifra výsledku, zvyšok X po delení 110 je nový zvyšok, s
ktorým pokračuješ ďalej.
Pre 1/110 takto dostávaš postupne zvyšky 1, 10, 100, 10... a v
tomto okamihu môžeš prestať počítať, lebo je jasné, že
zvyšky 10 a 100 sa budú dokola opakovať.
Krok 2: Ak navyše o našej postupnosti vecí vieš, že je len
konečne veľa možných vecí, tak sa v nekonečnej postupnosti skôr
či neskôr nejaký zopakuje, a preto je každá takáto postupnosť
nutne (niekedy časom, možno s nejakou predperiódou ako pri 1/110)
periodická.
Príklad: pri počítaní 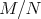 pre ľubovoľné kladné celé pre ľubovoľné kladné celé 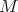 , , 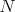 sú možné zvyšky len z množiny sú možné zvyšky len z množiny 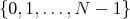 , teda ich je konečne veľa. Preto sa pri rátaní , teda ich je konečne veľa. Preto sa pri rátaní 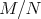 nutne zacyklíme, a v tomto cykle pridávame do výsledku dokola
stále tie isté cifry. Preto má každé racionálne číslo
periodický rozvoj v desiatkovej sústave. nutne zacyklíme, a v tomto cykle pridávame do výsledku dokola
stále tie isté cifry. Preto má každé racionálne číslo
periodický rozvoj v desiatkovej sústave.
Krok 3: No a posledná dobrá vlastnosť, ktorú môže takáto
postupnosť mať: ak z každého jej členu vieme určiť nie len
nasledujúci, ale aj predchádzajúci. Potom totiž prvý člen,
ktorý sa zopakuje, musí nutne byť úplne prvý člen celej
postupnosti. Prečo? Nech pre nejaké 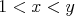 je je  -tý člen rovnaký ako -tý člen rovnaký ako 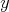 -ty. Potom je ale -ty. Potom je ale  -vý člen rovnaký ako -vý člen rovnaký ako  -vý, a tak ďalej, až prvý člen je rovnaký ako -vý, a tak ďalej, až prvý člen je rovnaký ako 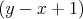 -vý -- a teda sa už prvý člen nutne niekde skôr zopakoval. -vý -- a teda sa už prvý člen nutne niekde skôr zopakoval.
Príklad: Máme v kruhu 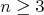 stoličiek. Ja si na nejakú sadnem, a následne dokola opakujem:
zdvihnem sa, prejdem o 3 stoličky ďalej v smere ručičiek, a tam si
sadnem. Potom prvá stolička, na ktorej budem sedieť druhýkrát, je
nutne tá, kde som začínal. stoličiek. Ja si na nejakú sadnem, a následne dokola opakujem:
zdvihnem sa, prejdem o 3 stoličky ďalej v smere ručičiek, a tam si
sadnem. Potom prvá stolička, na ktorej budem sedieť druhýkrát, je
nutne tá, kde som začínal. cituj ma |
| |
| Nena - 11. 10. 2009 - 23:24:36 z adsl-dyn69.78-98-27.t-com.skja chcem vedieť ako to malo byť, prosíím :) cituj ma |
| Mato - 11. 10. 2009 - 21:12:02 z dial-92-52-43-6-orange.orange.skStravil som bezsennu hodinku nad tymto prikladom ale s inou otazkou,
konkretne ze po kolkych krokoch skonci...potom som si precital zadanie
este raz a hned to slo.. cituj ma |
| Petržlen <petrzlen~kms~sk> - 11. 10. 2009 - 18:14:13 z adsl-dyn115.78-99-72.t-com.skPošlite nejaký fídbek k tomuto príkladu... bol ťažký, ľahký,
strávil som bezsenné noci nad ním a nedal som ho... :) cituj ma |
|
|
 |
|
|



