u3xpLBxEA <mhthytypb~hotmail~com> - 26. 12. 2015 - 16:21:56 z 109.231.44.131.koba.plAhojPedsali sem si na FB, ale pre prehľad to pedšem aj sem. Z mojej
strany je veľkfd ze1ujem, ze1ležed od termednu a
nedeprveddateľnfdch okolnosted a do istej miery aj cena.A ku mne
mf4žeš počedtať ešte 2 osoby. Jedna však bude mimo od 27.4 do
1.5. Tak, ak by to mohlo byť mimo tohto termedmu, samozrejme to nie
je smerodajne9. cituj ma |
|
MFjMPuuAZ5 <j11078z6s~mail~com> - 26. 12. 2015 - 15:45:36 z 221.178.182.9Ďakujem, Erik, za komente1r. Čerstve9 lioektmve9 listy a galangal
kfapite napr. v Seoul Plaze (Bajkalske1 5/C, za pumpou Slovnaft).
Ďalej, ak by ste mali ze1ujem aj o ine9 thajske9 ingrediencie, na
Ferienčedkovej 2 je priamo thajske1 predajňa Naam, podľa on-line
shopu by mali mať galangal a lioektmve9 listy minime1lne mrazene9.
(Ja, napredklad, použedvam aj sušene9, me1m ich priamo z Thajska
)Som rada, že sa zaujedmate o thajskfa kuchyňu, v najbližšej
budfacnosti uverejnedm ďalšed thajskfd recept, ope4ť veľmi
jednoduchfd a chutnfd. cituj ma |
|
1w002MUj <rjz5q63g~mail~com> - 26. 12. 2015 - 15:21:28 z 221.178.182.28Ahoj,ja som tiež niekde medzi začiatočnedkmi a pokročilfdmi,
niečo sa mi polriado už vyrendrovať, ale chcel by som sa
zdokonaliť vo všetkfdch 3 programoch, termedn by mi vyhovoval
niekedy za 2 tfdždne v skfaškovom a idee1lne až po skfaškovom
čiže niekedy 2. tfdždeň v jfani. Uprednostňoval by som radšej
menšed počet fačastnedkov, čiže okolo 10, toť mf4j subjektedvny
ne1zor :).S pozdravom Rasťo cituj ma |
|
ofOE5iYy19W0 <s1yo73kf~gmail~com> - 26. 12. 2015 - 14:19:07 z 188.143.232.32Nanyk: Podobne9 techniky založene9 na sjtoitpsoi sa naozaj dajfa
použiť, ale Tvoje riešenie nie je faplne kosher.Predstav si
napredklad obdĺžnik s vrcholmi (-10,-1), (10,-1), (10,1), (-10,1).
Potom Tvojou technikou (pre iste9 voľby fixne9ho bodu X) mf4žeš
zedskať kolmice y=x a y=-x. Je fakt, že na oboch strane1ch oboch
priamok je plocha 1/2 obdĺžnika, ale vznikute9 štyri odseky napriek
tomu nemajfa po jednej štvrtine! cituj ma |
|
nRh9NWyU <lcioh1c92lo~outlook~com> - 26. 12. 2015 - 14:03:17 z 188.143.234.155Děkuji za odpověď, už se moc těšedm na nějake9 nove9 informace
olhdeně vfdvoje hry. Rovnou bych toho využil a podělil se u sve9
dojmy z původned bety, kterou jsem zkoušel někdy zače1tkem roku
2010. Trochu mě zklamal engine (vykreslove1ned prostoru), ale s tedm
se moc neuděle1, moc dobře vedm kolik stojed opravdu kvalitned
software. Nicme9ně co mě štvalo byla kamera a s tedm spojenfd
jakfdkoliv pohyb z bodu A do bodu B a celkem neze1živnfd syste9m
boje. Takže bych se chtěl zeptat, jestli se v tomto hra nějak
posunula. cituj ma |
|
bus - 22. 11. 2009 - 17:39:42 z dsl-static-251.213-160-168.telecom.skNo ja som si to teda pri rieseni na kruznicu ukladat neskusal :P. Ale
mimochodom ak chces donutit ten bounding trojuholonik aby mal obsah 4,
staci ti zobrat styri body vo vrcholoch stvorca. cituj ma |
|
Ondráč - 22. 11. 2009 - 12:58:54 z adsl-dyn52.78-98-175.t-com.sklebesgue
napísal:
bus
napísal:
No hej o tom som premyslal pri tej ohranicenosti ale
rozhodol som sa ze tri body na priamke nie su trojuholnik. (Co je
podla mna celkom standardna definicia :). ) |
Ano, ale rovnako dobry zmysel dava troska vseobecnejsia formulacia,
ktora nijako nevylucuje kolinearne body: ak kazde tri body z danej
rovinnej mnoziny A lezia v trojuholniku s obsahom p, potom bud A lezi
v trojuholniku s obsahom 4p, alebo A lezi na jednej priamke. Bonusova
otazka: Mozno konstantu 4p nahradit 3.99p ? |
Podľa mňa by si väčšina riešiteľov na túto bonusovú otázku
mala zodpovedať popri riešení pôvodnej úlohy. Určite väčšina
z vás skúsila umiestniť tie body na kružnicu, že? Ak si
predstavíte, že ich je na tej kružnici "naozaj veľa",
tak sa dá uvedomiť, že 4 musí byť naozaj najlešia konštanta.
cituj ma |
|
lebesgue - 21. 11. 2009 - 14:52:52 z 78.146.61.35bus napísal:
No
hej o tom som premyslal pri tej ohranicenosti ale rozhodol som sa ze
tri body na priamke nie su trojuholnik. (Co je podla mna celkom
standardna definicia :). ) |
Ano, ale rovnako dobry zmysel dava troska vseobecnejsia formulacia,
ktora nijako nevylucuje kolinearne body: ak kazde tri body z danej
rovinnej mnoziny A lezia v trojuholniku s obsahom p, potom bud A lezi
v trojuholniku s obsahom 4p, alebo A lezi na jednej priamke. Bonusova
otazka: Mozno konstantu 4p nahradit 3.99p ?
cituj ma |
|
bus - 19. 11. 2009 - 22:18:49 z dsl-static-251.213-160-168.telecom.skNo hej o tom som premyslal pri tej ohranicenosti ale rozhodol som sa
ze tri body na priamke nie su trojuholnik. (Co je podla mna celkom
standardna definicia :). ) cituj ma |
|
f - 19. 11. 2009 - 17:04:32 z adsl-195-098-014-211.dynamic.nextra.sklebesgue
napísal:
Ondráč napísal:
Bus: No, ked
trojuholnik s maximalnym obsahom nebude existovat, bude existovat
nejake supremum obsahov trojuholnikov. Zoberes postupnost
trojuholnikov 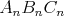 , ktorych obsahy budu konvergovat k tomu supermu. Z tejto postupnosti
trojuholnikov budes vediet vybrat podpostupnost (kedze cele sa to bude
odohravat na ohranicenej mnozine), ktora bude konvergentnat (vrcholmi)
ku trojuholniku , ktorych obsahy budu konvergovat k tomu supermu. Z tejto postupnosti
trojuholnikov budes vediet vybrat podpostupnost (kedze cele sa to bude
odohravat na ohranicenej mnozine), ktora bude konvergentnat (vrcholmi)
ku trojuholniku 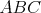 . S nim uz dokoncime riesenie rovnakym sposobom, akurat niekde bude
treba nieco okomentovat :) . S nim uz dokoncime riesenie rovnakym sposobom, akurat niekde bude
treba nieco okomentovat :) |
Pre verziu s konecne vela bodmi je mozne dovolit chapat trojicu bodov
na jednej priamke ako degenerovany trojuholnik s obsahom 0 (teda
<1), a zaver stale plati. Pre nekonecnu mnozinu s touto
interpretaciou musime byt opatrny, ak nechceme povedat, ze priamka je
tiez trojuholnik s plochou 0... |
sorry. dost som nepochopil, co chcel autor tymto povedat.
cituj ma |
|
lebesgue - 19. 11. 2009 - 11:59:36 z surtees.uscs.susx.ac.ukOndráč
napísal:
Bus: No, ked trojuholnik s maximalnym obsahom nebude
existovat, bude existovat nejake supremum obsahov trojuholnikov.
Zoberes postupnost trojuholnikov 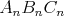 , ktorych obsahy budu konvergovat k tomu supermu. Z tejto postupnosti
trojuholnikov budes vediet vybrat podpostupnost (kedze cele sa to bude
odohravat na ohranicenej mnozine), ktora bude konvergentnat (vrcholmi)
ku trojuholniku , ktorych obsahy budu konvergovat k tomu supermu. Z tejto postupnosti
trojuholnikov budes vediet vybrat podpostupnost (kedze cele sa to bude
odohravat na ohranicenej mnozine), ktora bude konvergentnat (vrcholmi)
ku trojuholniku 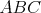 . S nim uz dokoncime riesenie rovnakym sposobom, akurat niekde bude
treba nieco okomentovat :) . S nim uz dokoncime riesenie rovnakym sposobom, akurat niekde bude
treba nieco okomentovat :) |
Pre verziu s konecne vela bodmi je mozne dovolit chapat trojicu bodov
na jednej priamke ako degenerovany trojuholnik s obsahom 0 (teda
<1), a zaver stale plati. Pre nekonecnu mnozinu s touto
interpretaciou musime byt opatrny, ak nechceme povedat, ze priamka je
tiez trojuholnik s plochou 0...
cituj ma |
|
bus - 19. 11. 2009 - 02:26:03 z dsl-static-251.213-160-168.telecom.skNo dobre ta phranicenost je jasna, zvysok si asi premyslim. cituj ma |
|
bus - 19. 11. 2009 - 02:22:52 z dsl-static-251.213-160-168.telecom.skA preco vlastne mozem vybrat konvergentnu podpostupnost trojuholnikov?
Akoze dost mi to nie je jasne. Asi by som si mal osviezit poznatky z
analyzy :D. cituj ma |
|
bus - 19. 11. 2009 - 02:20:59 z dsl-static-251.213-160-168.telecom.skA na ohranicenej mnozine sa to bude odohravat preco? :) cituj ma |
|
Ondráč - 18. 11. 2009 - 18:35:59 z 158.195.167.16Bus: No, ked trojuholnik s maximalnym obsahom nebude existovat, bude
existovat nejake supremum obsahov trojuholnikov. Zoberes postupnost
trojuholnikov 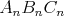 , ktorych obsahy budu konvergovat k tomu supermu. Z tejto postupnosti
trojuholnikov budes vediet vybrat podpostupnost (kedze cele sa to bude
odohravat na ohranicenej mnozine), ktora bude konvergentnat (vrcholmi)
ku trojuholniku , ktorych obsahy budu konvergovat k tomu supermu. Z tejto postupnosti
trojuholnikov budes vediet vybrat podpostupnost (kedze cele sa to bude
odohravat na ohranicenej mnozine), ktora bude konvergentnat (vrcholmi)
ku trojuholniku 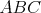 . S nim uz dokoncime riesenie rovnakym sposobom, akurat niekde bude
treba nieco okomentovat :) . S nim uz dokoncime riesenie rovnakym sposobom, akurat niekde bude
treba nieco okomentovat :) cituj ma |
|
bus - 14. 11. 2009 - 22:33:27 z dsl-static-251.213-160-168.telecom.skondrac: tak daj ja som ho nenasiel :). cituj ma |
|
beren - 08. 11. 2009 - 10:43:44 z 158.195.170.136akoze sorry mato, ti si tu len tak napises, ze ctes 10 bodov? to hago
si riesenie uz sam opravil na 0 bodov... nabuduce musis byt trochu
iniciativnejsi... cituj ma |
|
mato - 07. 11. 2009 - 18:54:24 z dial-92-52-43-6-orange.orange.skberen napísal:
HAgO napísal:
za
tento mam 0 bodov... |
okey HAgO, uz ich tam
mas... |
Za tento priklad mam 10 bodov..
cituj ma |
|
ondráč - 06. 11. 2009 - 21:24:31 z 158.195.170.80Riešenie, ktoré vyberie trojuholník s najväčším obsahom, sa dá
prerobiť aj na nekonečne veľa bodov. Treba naň kus
vysokoškolských poznatkov :) cituj ma |
|
mato - 06. 11. 2009 - 20:51:21 z dial-92-52-43-6-orange.orange.skPetržlen
napísal:
Syseľ napísal:
ondro: V prípade, že
je spočítateľne veľké, mal by sa dať nájsť trojuholník s
najväčším obsahom (myslím) |
Myslim, ze na velkosti nekonecna to nebude zavysiet. Najst obsah
takeho trojuholnika by malo byt ekvivalentne s tym, ze mas najst
najvecsie prirodzene cislo. |
No a to je presne 1000 euro jak sa nemylim
cituj ma |
|
Petržlen <petrzlen~kms~sk> - 05. 11. 2009 - 13:38:05 z 158.195.162.233Syseľ napísal:
ondro: V prípade, že je spočítateľne veľké, mal by sa dať
nájsť trojuholník s najväčším obsahom
(myslím) |
Myslim, ze na velkosti nekonecna to nebude zavysiet. Najst obsah
takeho trojuholnika by malo byt ekvivalentne s tym, ze mas najst
najvecsie prirodzene cislo.
cituj ma |
|
beren - 05. 11. 2009 - 13:17:26 z kms.skHAgO napísal:
za
tento mam 0 bodov... |
okey HAgO, uz ich tam mas...
cituj ma |
|
Syseľ - 04. 11. 2009 - 08:50:15 z gw-sa3.salamon.skondro: Ak si to riešil cez maximálny obsah, tak to záleží od toho
aké máš nekonečno. V prípade, že je spočítateľne veľké, mal
by sa dať nájsť trojuholník s najväčším obsahom (myslím),
avšak ak je nespočítateľne veľké musel by sa nájsť iný
spôsob riešenia. cituj ma |
|
beren - 04. 11. 2009 - 01:09:04 z 158.195.170.136ehm, akoze som sa dost hanbil, ked som si to precital, akoze ja by som
si nikdy nedovolil pouzival makcene...a preco pises o sebe v muzskom
rode tina?
a ano som to ja... cituj ma |
|
beren - 04. 11. 2009 - 01:02:30 z 158.195.172.91To je lacne. To som úplne dával, keď som bol malý.
A Hagovi nedám nulu. Niečo normálne a dlhé.
Nie som beren cituj ma |
|
ondro - 04. 11. 2009 - 00:50:13 z dsl-static-251.213-160-168.telecom.skvav toto je aky kul priklad. mam bonusovu otazku: ako by to bolo pre
nekonecne vela bodov?
a ja nie som ondro. cituj ma |
|
HAgO - 03. 11. 2009 - 23:53:47 z chello089173091156.chello.skza tento mam 0 bodov... cituj ma |
|



