Zadanie:
Číselným trojuholníkom nazveme útvar zložený z prirodzených
čísel, ktorý má tvar trojuholníka. V prvom riadku číselného
trojuholníka je  čísel, kde čísel, kde  je prirodzené číslo. Toto číslo je prirodzené číslo. Toto číslo  je zároveň dĺžkou strany číselného trojuholníka. Číselný
trojuhoník so stranou je zároveň dĺžkou strany číselného trojuholníka. Číselný
trojuhoník so stranou  má má  riadkov, pričom v riadkov, pričom v 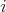 -tom riadku je -tom riadku je 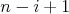 čísel. Čísla v dvoch po sebe idúcich riadkoch čísel. Čísla v dvoch po sebe idúcich riadkoch 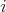 a a  sú umiestnené tak, že pod každou dvojicou čísel v sú umiestnené tak, že pod každou dvojicou čísel v 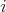 -tom riadku je číslo v -tom riadku je číslo v  -vom riadku. Číselný trojuholník voláme podivný, ak
platí: -vom riadku. Číselný trojuholník voláme podivný, ak
platí:
- čísla, ktoré ho tvoria, sú navzájom rôzne prirodzené
čísla,
- pod každou dvojicou susedných čísel v riadku
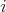 je číslo v riadku je číslo v riadku  , ktoré je podielom väčšieho a menšieho čísla z danej dvojice.
Toto platí pre všetky , ktoré je podielom väčšieho a menšieho čísla z danej dvojice.
Toto platí pre všetky 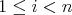 , kde , kde  je dĺžka strany číselného trojuholníka. je dĺžka strany číselného trojuholníka.
Napríklad číselný trojuholník na nasledujúcom obrázku je
podivný.
Najväčšie číslo v podivnom číselnom trojuholníku nazveme
úžasné. Nájdite číselný trojuholník s dĺžkou strany
4, ktorého úžasné číslo je čo najmenšie. Dokážte, že
neexistuje číselný trojuholník s dĺžkou strany 4 a s menším
úžasným číslom, ako ste našli. |



