|
|
 |
9. príklad 1. letnej série 2008/2009
Zadanie:
Nech  je prirodzené číslo, ktoré je aspoň 3. Nech je prirodzené číslo, ktoré je aspoň 3. Nech 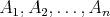 sú navzájom rôzne podmnožiny množiny sú navzájom rôzne podmnožiny množiny  . Dokážte, že vždy existuje . Dokážte, že vždy existuje 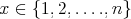 také, že keď z každej množiny také, že keď z každej množiny 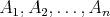 odoberieme odoberieme  , tak novovzniknuté množiny sú tiež navzájom rôzne. (Ak sa , tak novovzniknuté množiny sú tiež navzájom rôzne. (Ak sa  v niektorej z množín nenachádza, tak táto množina ostane
rovnaká.) v niektorej z množín nenachádza, tak táto množina ostane
rovnaká.) |
bus - 09. 03. 2009 - 23:55:51 z dsl-static-251.213-160-168.telecom.skTo nikto nedokazete ocenit eleganciu a zbytocnost s ktorou sa da
aplikovat vysokoskolska matika na stredoskolsky problem? :D cituj ma |
| katka - 09. 03. 2009 - 18:47:25 z 158.195.167.67mne skor linearnu algebru :) cituj ma |
| kamilama - 09. 03. 2009 - 16:58:15 z 158.196.244.87.in-addr.arpatoto mi skor evokuje nejaku fyziku zmiesanu s informatikou :D:D cituj ma |
| mišof - 04. 03. 2009 - 00:04:46 z adsl-dyn70.78-99-45.t-com.skTeda napadlo ma také jedno brutálne, až sa hanbím.
Každú podmnožinu  môžeme reprezentovať ako vektor môžeme reprezentovať ako vektor  núl a jednotiek (zapíšeme, ktoré prvky v nej sú a ktoré nie).
Nech núl a jednotiek (zapíšeme, ktoré prvky v nej sú a ktoré nie).
Nech  sú vektory popisujúce sú vektory popisujúce  . .
Prvok  je zlý, ak existujú je zlý, ak existujú 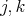 také, že také, že  je je  -tý jednotkový vektor -- t.j. vektor, ktorý má všade -tý jednotkový vektor -- t.j. vektor, ktorý má všade 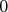 , len na , len na  -tej pozícii -tej pozícii  . .
Uvažujme  vektorov: vektorov: 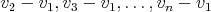 . Táto množina vektorov generuje nejaký najviac . Táto množina vektorov generuje nejaký najviac  rozmerný vektorový priestor rozmerný vektorový priestor 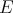 . .
V priestore 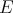 sú okrem iného aj všetky vektory tvaru sú okrem iného aj všetky vektory tvaru  , lebo , lebo  . .
Ak by každé  bolo zlé, tak by v bolo zlé, tak by v 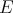 muselo byť všetkých muselo byť všetkých  jednotkových vektorov, a teda by jednotkových vektorov, a teda by 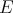 bol bol  -rozmerný. To ale nie je pravda. -rozmerný. To ale nie je pravda.
(Hmm, fakt sa to nedá porovnateľne stručne povedať stredoškolskou
matikou? Lama som...) cituj ma |
| mišof - 03. 03. 2009 - 23:52:11 z adsl-dyn70.78-99-45.t-com.skNo tak elegantné riešenie uniká aj mne. Umlátiť to indukciou sa
dá, aj cez tie grafy sa dá, ale ono to vyzerá, že by to malo mať
nejaké riešenie, že dve vety a hotovo, a také nevidim a
nevidííím :P cituj ma |
| Kubo - 27. 02. 2009 - 18:11:14 z adsl-dyn50.78-98-16.t-com.skAko ste to robili? lebo mne sa moje riesenie cez grafy zda divne...
ale zato spravne ale aj tak divne cituj ma |
|
|
 |
|
|



