Zadanie:
Sinetu s Montym nachystali na Drzohubých dokonalú pascu. Dva
najvzácnejšie body galérie dali do jednej malej miestnosti. Dosť
malej na to, aby okolo nej zvládli nainštalovať skryté
bezpečnostné mreže. Jeden z bodov (slávny Whistlerov bod) bol
navyše upevnený na špeciálnom závite, na ktorého odšróbovanie
treba presne toľko ľudí, koľko má celá banda Krivozubého
Tonyho. Večer pred lúpežou sa Monty schoval v miestnosti
s dvoma vzácnymi bodmi (druhým z bodov bola vzácna Mona
Bod s potmehútskym úsmevom), aby mohol v správny čas
spustiť mreže. Miestnosť mala tvar rovnoramenného pravouhlého
trojuholníka s pravým uhlom pri bode 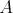 . Oba vzácne body . Oba vzácne body 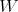 a a 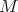 ležali na strane ležali na strane 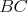 . Navyše si Montyho zrak pravého kovboja všimol dve zaujímavosti.
Za prvé to, že platilo . Navyše si Montyho zrak pravého kovboja všimol dve zaujímavosti.
Za prvé to, že platilo 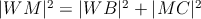 a za druhé, že a za druhé, že 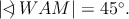 Dokážte, že to nie je náhoda, t.j., že Dokážte, že to nie je náhoda, t.j., že 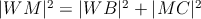 práve vtedy, keď práve vtedy, keď 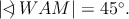
|



