|
|
 |
10. príklad 3. zimnej série 2009/2010
Syseľ - 01. 12. 2009 - 17:53:00 z gw-sa3.salamon.skSyseľ napísal:
...
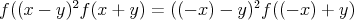
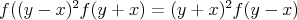
...
|
Prepáčte v týchto výrazoch je chyba, tu sú opravené:
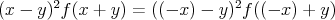
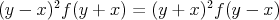
cituj ma |
| Syseľ - 01. 12. 2009 - 17:47:50 z gw-sa3.salamon.skMajme dve rovnice:
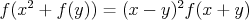

Pravé strany sa rovnajú => rovnajú sa aj ľavé:
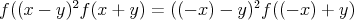
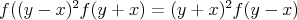
Nech 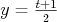 a a 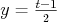 potom potom 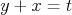 a a 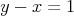 teda : teda :
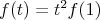
kde 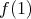 je konštanta, ktorej hodnotu zistíme po dosadení do prvej rovnice
( je konštanta, ktorej hodnotu zistíme po dosadení do prvej rovnice
( 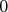 , ,  ) )
teda 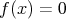 alebo alebo 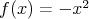 . .
:-) cituj ma |
| Nena - 01. 12. 2009 - 14:03:54 z adsl-dyn246.78-98-171.t-com.skmoje riešenie sa mi páčilo, to bude asi tým, že mám len
začiatok.. :D cituj ma |
| mato - 01. 12. 2009 - 13:30:38 z dial-92-52-43-6-orange.orange.skNa zaciatku riesenia sa mi to pacilo ale potom sa to zvrhlo... cituj ma |
|
|
 |
|
|



