Zadanie:
Maťo si vytvoril postupnosť prirodzených čísel  nasledovným spôsobom: zvolil si najprv prirodzené číslo nasledovným spôsobom: zvolil si najprv prirodzené číslo 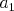 a ďalšie členy postupnosti určil podľa vzťahu a ďalšie členy postupnosti určil podľa vzťahu 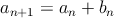 , kde , kde 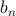 je posledná cifra čísla je posledná cifra čísla 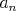 , pre všetky prirodzené čísla , pre všetky prirodzené čísla  . Dokážte, že Maťova postupnosť obsahuje nekonečne veľa
celočíselných mocnín dvojky práve vtedy, keď . Dokážte, že Maťova postupnosť obsahuje nekonečne veľa
celočíselných mocnín dvojky práve vtedy, keď 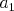 nie je deliteľné piatimi. nie je deliteľné piatimi.
|



