Zadanie:
Drak má v jaskyni zaujímavú dvojicu trojuholníkov. Platí pre ne,
že dve strany jedného trojuholníka sú rovnako dlhé ako niektoré
dve strany druhého trojuholníka a že trojuholníky sú podobné
(ale nie nutne zhodné). Drak hrdo vyslovil nasledujúce tvrdenie:
Keby som mal hocijakú dvojicu trojuholníkov s takýmito
vlastnosťami, tak koeficient podobnosti týchto trojuholníkov by
bolo číslo medzi 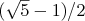 a a  a nebolo by rovné týmto krajným hodnotám. Dokážte, že drak
má pravdu. a nebolo by rovné týmto krajným hodnotám. Dokážte, že drak
má pravdu. |



