Zadanie:
Na matfyze v Sydney majú každí dvaja študenti, ktorí sa navzájom
nepoznajú, aspoň jedného spoločného známeho (poznanie sa je
symetrické). Ani jeden študent pritom nepozná všetkých
ostatných. Očíslujme študentov od  po po  a nech a nech 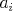 označuje počet známych označuje počet známych 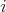 -teho študenta. Vieme, že platí -teho študenta. Vieme, že platí
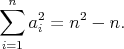
Nech  je najmenší počet študentov, ktorých možno usadiť okolo
okrúhleho stola tak, aby každý poznal oboch svojich susedov.
Nájdite všetky možné hodnoty je najmenší počet študentov, ktorých možno usadiť okolo
okrúhleho stola tak, aby každý poznal oboch svojich susedov.
Nájdite všetky možné hodnoty  . . |



