Zadanie:
Bod 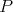 leží vnútri štvorca leží vnútri štvorca 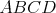 . Označme . Označme 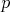 a a 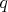 rovnobežky so stranami
tohto štvorca prechádzajúce bodom rovnobežky so stranami
tohto štvorca prechádzajúce bodom 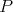 . Ďalej označme . Ďalej označme  a a  rovnobežky
s uhlopriečkami štvorca opäť prechádzajúce bodom rovnobežky
s uhlopriečkami štvorca opäť prechádzajúce bodom 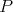 . Priamky . Priamky 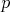 , , 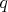 , ,  a a
 celkovo rozdelia štvorec celkovo rozdelia štvorec 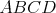 na 8 častí. Ofarbime teraz tieto časti
striedavo modrou a červenou farbou tak, aby každé dve časti
susediace stranou
mali rôznu farbu. Dokážte, že súčet obsahov častí, ktoré sú
ofarbené na modro,
je polovica z obsahu štvorca na 8 častí. Ofarbime teraz tieto časti
striedavo modrou a červenou farbou tak, aby každé dve časti
susediace stranou
mali rôznu farbu. Dokážte, že súčet obsahov častí, ktoré sú
ofarbené na modro,
je polovica z obsahu štvorca 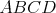 . . |



