Zadanie:
Hago napísal na tabuľu jedno prirodzené číslo tvaru 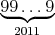 .
Potom prišiel k tabuli Edo a opakoval svoj ťah
pozostávajúci z nasledujúcich krokov: .
Potom prišiel k tabuli Edo a opakoval svoj ťah
pozostávajúci z nasledujúcich krokov:
- Vybral si jedno z prirodzených čísel na tabuli a označil ho
 . V prvom ťahu práve . V prvom ťahu práve  . .
- Zvolil si prirodzené čísla
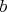 a a  také, že také, že  . .
- Od čísla
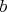 odčítal alebo pričítal odčítal alebo pričítal 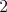 a získal tým číslo a získal tým číslo 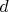 a od čísla a od čísla  odčítal alebo pričítal odčítal alebo pričítal 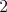 a získal tým číslo a získal tým číslo  . .
- Z tabule zmazal pôvodné číslo
 a napísal namiesto neho čísla a napísal namiesto neho čísla 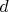 a a  . .
Je možné, aby po niekoľkých Edových ťahoch zostali na tabuli len
čísla 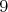 ? ? |



