Zadanie:
Máme kružnice  a a 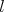 , ktoré sa dotýkajú v bode , ktoré sa dotýkajú v bode 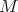 . Ďalej máme dotyčnicu . Ďalej máme dotyčnicu 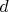 ku kružnici ku kružnici 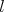 , ktorá pretína kružnicu , ktorá pretína kružnicu  . Označme . Označme 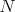 bod dotyku dotyčnice bod dotyku dotyčnice 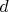 s kružnicou s kružnicou 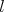 a priesečníky dotyčnice a priesečníky dotyčnice 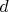 s kružnicou s kružnicou  označme označme 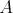 a a 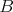 . Priesečník priamky . Priesečník priamky 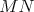 s kružnicou s kružnicou  rôzny od rôzny od 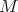 označme označme 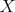 . Dokážte, že . Dokážte, že 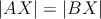 . .
|



