Zadanie:
Mojo našiel v školskom sklade tabuľku 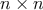 . Na každom políčku tabuľky bola lampa. Na začiatku boli všetky
lampy vypnuté. Potom sa s ňou Mojo začal hrať. V každom
ťahu si vybral v riadku alebo stĺpci . Na každom políčku tabuľky bola lampa. Na začiatku boli všetky
lampy vypnuté. Potom sa s ňou Mojo začal hrať. V každom
ťahu si vybral v riadku alebo stĺpci 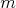 po sebe idúcich lámp a zmenil stav týchto lámp (zo zapnutej
na vypnutú a naopak). Dokážte, že stav, v ktorom sú
všetky lampy zapnuté, vie Mojo dosiahnuť práve vtedy, keď číslo po sebe idúcich lámp a zmenil stav týchto lámp (zo zapnutej
na vypnutú a naopak). Dokážte, že stav, v ktorom sú
všetky lampy zapnuté, vie Mojo dosiahnuť práve vtedy, keď číslo
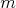 je deliteľom čísla je deliteľom čísla  . .
|



