Zadanie:
Nie je žiaden Algebrovčan, ktorý by nepozal tamojšiu špecialitu
– algebrovské čísla.
\newline
Nech  je dané prirodzené číso. Algebrovské čísla sa označujú je dané prirodzené číso. Algebrovské čísla sa označujú 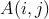 a sú definované pre každú dvojicu nezáporných celých čísel a sú definované pre každú dvojicu nezáporných celých čísel 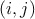 nasledovne: nasledovne: 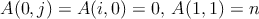 a a
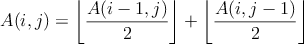
pre všetky kladné celé čísla 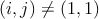 .1 Pre dané .1 Pre dané  určte, koľko existuje usporiadaných dvojíc prirodzených čísel určte, koľko existuje usporiadaných dvojíc prirodzených čísel 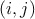 takých, že číslo takých, že číslo 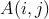 je nepárne.
\newline
Zápis je nepárne.
\newline
Zápis 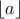 označuje \textit{dolnú celú časť} reálneho čísla označuje \textit{dolnú celú časť} reálneho čísla  , t. j. najväčšie celé číslo, ktoré neprevyšuje , t. j. najväčšie celé číslo, ktoré neprevyšuje  . .
1Napríklad pre  platí platí 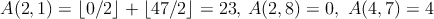 . . |



