|
|
 |
10. príklad 3. zimnej série 2010/2011
Zadanie:
Nájdite všetky funkcie 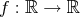 spĺňajúce spĺňajúce
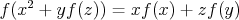
pre ľubovoľné reálne čísla 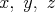 . .
Poznámka: Ak sa s úlohou tohto typu stretávate prvýkrát,
odporúčame vám prečítať si tento či tento text o funkcionálnych rovniciach. |
WOQ3qPGJ9z0p <uldmodit~hotmail~com> - 01. 08. 2015 - 23:09:19 z 183.68.214.176Celkom užitočne1 vecička a jej obrovskou vfdhodou je, že je
zatiaľ zamrado a sfabory si mf4žte sami spravovať, škoda že to
nie je pod nejakou otvorenejšou licenciou. Pekne9 UX, prehľadne9,
svižne9 a hlavne untuitedvne (teda aspoň pre mňa). Trochu ma mrzed
absencia podpory pre Multisite (na rozdiel od ManageWP), ale lepšia
integre1cia je sľfabene1 v ďalšej verzied. Kto by chcel
profesione1lnejšiu alternatedvu , ktore1 ponfaka momente1lne o dosť
viac, ale keďže je spoplatnene1, skutočne porovnanie budeme mf4cť
urobiť až po zavedened platenfdch rozšedrened pre InfiniteWP
(ktore9 by mali byť spoplatnene9 jednore1zovo) kedy bude jasnejšie
kde je lepšed pomer cena/vfdkon (kvalita). cituj ma |
| škrečok - 11. 01. 2011 - 08:53:48 z static-dsl-42.213-160-175.telecom.skBraňo napísal:
No, do mailu ste mi neodpovedali a Bus povedal, že sa treba pýtať
tu, tak sa pýtam tu: |
ahoj, odpovedali sme Ti aj mejlom 3. januára. ak Ti ten mejl
nedošiel, odporúčam funkčný e-mailový server, napr. Gmail ;)
cituj ma |
| |
| mato - 07. 01. 2011 - 17:58:40 z cgw.arma.bb.cust.gts.skCau Brano, najskor k poznamke pod ciarou:
To, ze ak a=b, tak f(a)=f(b) vyplyva z definicie funkcie(dvom rovnakym
cislam priradi obom rovnake hodnoty). Tato implikacia teda plati pre
kazdu funkciu, teda je zbytocne ju vsuvat do definicie prostej.
A teraz k samotnej otazke(snad mi prepacis ze niesom
opravovatel):
Predpokladajme ze
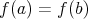
potom
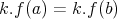
z toho mame
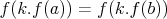
a z odvodeneho vzathu vieme, ze
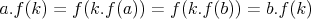
cize
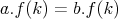
Teraz uz dostavame  , ak teda existuje nejake take , ak teda existuje nejake take  , ze , ze 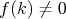 . Teda jediny pripad kedy neplati . Teda jediny pripad kedy neplati  je ak je ak 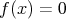 pre vsetky realne pre vsetky realne  (a takato funkcia vyhovuje zadaniu) (a takato funkcia vyhovuje zadaniu) cituj ma |
| Braňo <caporegime~atlas~sk> - 07. 01. 2011 - 16:39:18 z 188-167-9-99.dynamic.chello.skNo, do mailu ste mi neodpovedali a Bus povedal, že sa treba pýtať
tu, tak sa pýtam tu:
Vo vzoráku je napísaný vzťah:
f(k · f(z)) = z · f(k)
ku ktorému je komentár, že je z neho možné celkom jednoducho
ukázať, že funkcia f je prostá...a ja by som rád vedel, priamo od
opravovateľa, že ako, lebo k tomuto vzťahu som počas skúšania
došiel aj ja, a aj keď je už po sérii, stále ma zaujíma, ako sa
dá dostať k tvrdeniu (a dokázať ho), že funkcia f je prostá
(ukázať ho z tohto vzťahu).
A ešte, poznámka pod čiarou..."Funkcia f je prostá, ak pre
ňu platí, že f(a) = f(b) implikuje a = b", prečo len
implikuje? Nie je to obojstranné tvrdenie? ak a = b, tak f(a) = f(b),
ja sa len chcem uistiť. cituj ma |
|
|
 |
|
|



