|
|
 |
11. príklad 2. zimnej série 2012/2013
Zadanie:
Kružnica vpísaná trojuholníku 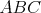 sa dotýka strán sa dotýka strán 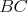 , , 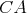 , , 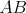 postupne v bodoch postupne v bodoch 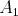 , , 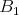 , , 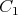 . Úsečka . Úsečka 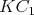 je priemerom tejto kružnice a bod je priemerom tejto kružnice a bod 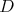 je priesečníkom priamok je priesečníkom priamok 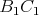 a a 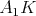 . Dokážte, že . Dokážte, že 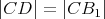 . . |
nkuBVvMJAwJj <2bf6cnpj1a0~gmail~com> - 21. 10. 2015 - 12:36:10 z 221.178.182.48Ejha :) tak predsa... Som rad, ze ste sa s tym takto ppolsovaai. A to
pribeh s diktatormi zdaleka nekonci. Teda, toto je len zaciatok celeho
badania :)Preformulujme si trosku zadanie. Namiesto toho, aby sa
nejaka nahodna dvojica planetok navzajom znicila, tak do seba naburaju
a vznikne tak dvojplanetka. (Dvojplanetky sa zatial spajat nemozu).
Zisili sme, ze na konci spajania sa planetok do dvojplanetok nam
zostane priblizne e^{-2} planetok a (1-e^{-2})/2 dvojplanetok.
Diktatori si uvedomia, ze by mohli vzniknut aj trojplanetky a tak
niektore nahodne dvojice susediacich planetok a dvojplanetok zacnu
vytvrat trojplanetky. Nahodny proces pokracuje az kym opat ziadna
trojplanetka nemoze vzniknut. Ake bude zastupenie planetok,
dvojplanetok a trojplanetok na konci tohoto procesu?V dalsom kroku si
pockame kym sa vytvoria vsetky mozne stvorplanetky, potom patplanetky,
... a ako spravny matematici, n-planetky. Pritom si po kazdom kroku do
nejakeho histogramu zakreslime ako vyzeraju stredne hodnoty zastupeni
jednotlivych velkosti. Tieto rozlozenia sa (po vhodnom preskalovani)
budu na seba velmi podobat, az si jeden zaumieni, ze by mohol dokazat,
ze sa blizia k nejakemu spojitemu rozdeleniu. Otazka znie, ake to
rozdelenie je :)Nas v praci az tak nezaujima, ako sa to sprava (tento
model tam nakoniec vobec nerozoberame), ale niekedy zo zaciatku sme si
na tomto ukazovali ako funguje "coagulation with maximal
size". Koho to trosku zaujalo, mozete si kuknut tak prve dve
stranky z www.lps.ens.fr/~boudaoud/Publis/Boudaoud07Aggreg.pdf cituj ma |
|
|
 |
|
|



