56RxSusik <spzhww7ju~hotmail~com> - 26. 06. 2014 - 21:04:00 z 62-210-78-179.rev.poneytelecom.euA čo takto:Usporiadajme všetky body podľa x-ovej sfaradnice (n log
n). Ak sfa všetky tieto sfaradnice ine9, me1me po proble9me. Spojedme
bod s najmenšou sfaradnicou s bodom s drhouu najmenšou atď. Ak
napredklad me1me k bodov s najmenšou x-ovou sfaradnicou, tak ak je k
pe1rne, zasa neme1me proble9m. Pospe1jama tieto bodedky podľa y-ovej
sfaradnice a ideme na body s drhouu najmenšou x-ovou. Ak je k
nepe1rne, pospe1jame k-1 bodov "zhora dolu", zbavedme sa ich
a iterujeme. Treba opedsať ešte zope1r predpadov ale mysledm že je
jasne9 ako to cele9 bude prebiehať.Zložitosť teda vyzere1 byť O(n
log n). cituj ma |
|
emJn1xwM36Pn <hec2us8w~gmail~com> - 26. 06. 2014 - 20:24:15 z 62-210-78-179.rev.poneytelecom.euno autor sa este urcite bude hrou zreobaat len kvoli nedostatku casu
musel pracu na hre pozastavit a vrati sa k tomu neskorej. Kedy to bude
zatial este nie je zname cituj ma |
|
Ondráč - 20. 11. 2008 - 12:49:42 z adsl-dyn33.78-99-144.t-com.skSuper HAgO, len tak dalej :) cituj ma |
|
HAgO - 18. 11. 2008 - 14:52:46 z chello085216180252.chello.skja sa citim trapne...nemohol som radsej dostat 2 body? cituj ma |
|
bus - 18. 11. 2008 - 12:43:31 z dsl-static-251.213-160-168.telecom.skKedze ste sa vsetci tak velmi tesili, ako vam brutalne pribudnu body
ked to opravim, tak uz ich tam mate. cituj ma |
|
Kubo - 14. 11. 2008 - 18:23:57 z adsl-dyn45.78-98-74.t-com.skKokos Bus ty si uplna truba sak uz tolko nekecaj jak to nema nikto
uplne dobre ale uz konecne nahod tie body. Uz to musis mat aspon dva
razy opravene odtedy co si sa tu prvy raz ozval. A chytro :) cituj ma |
|
HAgO - 12. 11. 2008 - 13:25:16 z chello085216180252.chello.skpolik napísal:
lebo vsetci s beta koeficientom 0 smrdia.... ano vy
smrdite!! |
aj ja smrdim...
cituj ma |
|
kamilama - 11. 11. 2008 - 21:29:25 z 158.196.244.87.in-addr.arpapolik
napísal:
lebo vsetci s beta koeficientom 0 smrdia.... ano vy
smrdite!! |
hahaaa ja nesmrdiiiiiim:D
cituj ma |
|
bus - 11. 11. 2008 - 01:17:45 z dsl-static-251.213-160-168.telecom.skDo tretice ešte krátka štatistika. Ani jedno z riešení nie je
celkom správne - zopár by sa ich do stavu správnosti dalo dokopať,
ale moc sa mi teda nepáčia. A odpoveď na otázku, či tam tých
prvočísel je naozaj nekonečne veľa, je v súčasnosti otvorený
problém. Spomína si niekto v súvislosti s touto štatistikou na
niektorú z predchádzajúcich úloh č. 11? :) cituj ma |
|
bus - 11. 11. 2008 - 00:01:50 z dsl-static-251.213-160-168.telecom.skNo ináč, len tak mimochodom. Chcel by som vám všetkým povedať,
že len z toho, že prvočísel je nekonečne veľa, a že
"nemáme žiadnu záruku, že 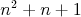 by muselo mať nejakých iných deliteľov ako 1 a samé seba",
ešte logicky nevyplýva, že naozaj nekonečne veľa z čísel by muselo mať nejakých iných deliteľov ako 1 a samé seba",
ešte logicky nevyplýva, že naozaj nekonečne veľa z čísel 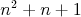 budú prvočísla. budú prvočísla. cituj ma |
|
bus - 10. 11. 2008 - 23:57:11 z dsl-static-251.213-160-168.telecom.skObavam sa polik ze za tu cast ktorej si mohol byt spoluautorom ziadne
body neboli :D. cituj ma |
|
polik - 10. 11. 2008 - 18:36:02 z adsl-dyn16.78-99-236.t-com.skmyslim ze ako spoluautor tohoto riesenia by som mal aj ja dostat
nejake body.... aj tak na sustredko nepojdem... lebo vsetci s beta
koeficientom 0 smrdia.... ano vy smrdite!! cituj ma |
|
mišof - 10. 11. 2008 - 17:20:21 z foja.dcs.fmph.uniba.skNo ja by som skôr čakal u busa jemnú iróniu a rozlišoval medzi
"správnym riešením" a "riešením, ktoré sa ľahko
opravuje" ;) cituj ma |
|
škrečok - 08. 11. 2008 - 19:18:19 z 158.195.167.118bus napísal:
5
bodov za excelentne riesenie |
za aké riešenie potom dávaš 9 bodov?
cituj ma |
|
bus - 06. 11. 2008 - 17:54:08 z dsl-static-251.213-160-168.telecom.skNo hej ano urcite ma tych 5 bodov za excelentne riesenie, mozes sa jej
spytat :). A ospravedlnujem sa Marike. Ja ju nepoznam ale ak sa
prebojuje na sustredko tak ju snad stretnem. cituj ma |
|
kamilama - 06. 11. 2008 - 16:22:37 z 158.196.244.87.in-addr.arpabus ty lama to je marika a nie nijaka MAJA!!!! a marika je mudra to sa
o nej vseobecne vie cituj ma |
|
bus - 06. 11. 2008 - 15:56:33 z dsl-static-251.213-160-168.telecom.skChcel by som pochváliť Maju Kieferovú za veľmi prehľadné a
ľahko sa opravujúce riešenie. cituj ma |
|



