Zadanie:
Daná je postupnosť nezáporných celých čísel  . Pre každé prirodzené . Pre každé prirodzené 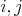 také, že také, že  , platí , platí
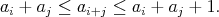
Dokážte, že existuje nekonečne veľa reálnych čísel  , pre ktoré platí , pre ktoré platí 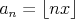 pre všetky pre všetky 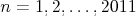 . .
Poznámka: 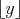 označuje dolnú celú časť z označuje dolnú celú časť z 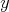 , teda najväčšie celé číslo menšie alebo rovné ako , teda najväčšie celé číslo menšie alebo rovné ako 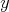 . . |



