|
|
 |
12. príklad 1. letnej série 2008/2009
Zadanie:
Do štvorčekov nekonečného štvorčekového papiera sú vpísané
reálne čísla. Dané sú dve šablóny zložené z konečného
počtu štvorčekov. Tieto šablóny môžeme posúvať pozdĺž čiar
na štvorčekovom papieri, nemeníme však ich orientáciu. Vieme, že
ak prvú šablónu priložíme na ľubovoľné miesto, súčet čísel
na políčkach, ktoré zakrýva, bude kladný. Dokážte, že existuje
také umiestnenie druhej šablóny, že súčet čísel na
políčkach, ktoré zakrýva, je tiež kladný. |
Kubo - 06. 03. 2009 - 22:36:09 z adsl-dyn50.78-98-16.t-com.skTo je nepekne. cituj ma |
| Ondráč - 03. 03. 2009 - 16:15:56 z 158.195.165.180Kubo napísal:
No
tak ja bych celkom rad vedel ze ci to mam dobre. Mozem sablonu polozit
vsade? Akoze ci mozem kazde policko mat na kazdom mieste sablony. A
potom z toho vyplyva ze sucet vsetkych policok je kladny. a Potom
rovnako s druhou sablonou spravim spor ze sucet vsetkych policok je
zaporny. Mozem robit taketo veci? |
S nepotešením ti musím oznámiť (aj ďalším trom), že toto sa
robiť nedá.
Keď položím prvú šablónu na ľubovoľné miesto, dostanem
kladný súčet. Keď sčítam nekonečne veľa kladných čísel,
dostanem buď kladné číslo, alebo nekonečno. Teda spokojne môžem
povedať
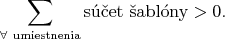
Vo všeobecnosti však neplatí, že takto sme dostali ( je počet políčok šablóny) je počet políčok šablóny)  -násobok súčtu všetkých políčok. Súčet políčok ani nemusí
existovať (v takom prirodzenom zmysle). Veď si to skúsme...
Vyfarbime si papier šachovnicovo a do čiernych políčok vpíšme
jednotky. Biele políčka si nejako usporiadajme a postupne do nich
vpisujme hodnoty -násobok súčtu všetkých políčok. Súčet políčok ani nemusí
existovať (v takom prirodzenom zmysle). Veď si to skúsme...
Vyfarbime si papier šachovnicovo a do čiernych políčok vpíšme
jednotky. Biele políčka si nejako usporiadajme a postupne do nich
vpisujme hodnoty  , ,  , ,  , pričom , pričom 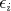 sú všetky kladné a platí sú všetky kladné a platí
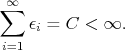
Ako prvú šablónu si zoberme štvorček  . Keď ho ľubovolne umiesnime, dostaneme kladný súčet ( . Keď ho ľubovolne umiesnime, dostaneme kladný súčet ( ). Súčet všetkých umiestnení tejto šablóny bude ). Súčet všetkých umiestnení tejto šablóny bude
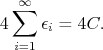
Skúste však nejakým spôsobom povedať, aký je súčet celej
šachovnice. Koľko to bude? Je to niečo ako sčitovať nekonečný
rad

tu však dokonca ani nemáte dané nejaké "poradie". Takže
hovoriť o súčte všetkých políčok je dosť vágne a chcelo by to
asi mnoho (alebo aj nekonečne veľa :)) úvah na doriešenie úlohy
takýmto prístupom.
cituj ma |
| Kubo - 03. 03. 2009 - 15:23:54 z stip-static-208.213-81-187.telecom.skNo tak ja bych celkom rad vedel ze ci to mam dobre. Mozem sablonu
polozit vsade? Akoze ci mozem kazde policko mat na kazdom mieste
sablony. A potom z toho vyplyva ze sucet vsetkych policok je kladny. a
Potom rovnako s druhou sablonou spravim spor ze sucet vsetkych policok
je zaporny. Mozem robit taketo veci? cituj ma |
|
|
 |
|
|



