Zadanie:
Štvorec je rozdelený na 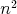 obdĺžnikov pomocou obdĺžnikov pomocou  zvislých a zvislých a  vodorovných úsečiek, kde vodorovných úsečiek, kde 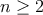 je celé číslo. Dokážte, že spomedzi nich vieme vybrať je celé číslo. Dokážte, že spomedzi nich vieme vybrať 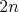 obdĺžnikov tak, aby pre ľubovoľné dva z nich platilo, že
jeden sa zmestí do druhého.1 obdĺžnikov tak, aby pre ľubovoľné dva z nich platilo, že
jeden sa zmestí do druhého.1
1Obdĺžniky možno aj otáčať. Dva zhodné obdĺžniky
sa zmestia do seba. Štvorec považujeme za špeciálny prípad
obdĺžnika. |



