|
|
 |
7. príklad 2. zimnej série 2008/2009
Zadanie:
Klokan má karty, na ktorých sú čísla od  po po  . Pozrie sa na prvú kartu.
Ak je na nej číslo . Pozrie sa na prvú kartu.
Ak je na nej číslo  , zmení zrkadlovo poradie prvých , zmení zrkadlovo poradie prvých  kariet. Takto
pokračuje až kým nedostane na prvej karte číslo kariet. Takto
pokračuje až kým nedostane na prvej karte číslo  . Musí sa mu to vždy po
konečnom počte krokov podariť? . Musí sa mu to vždy po
konečnom počte krokov podariť? |
en1FHomu4 <wiq8lt49oup~outlook~com> - 03. 03. 2014 - 15:45:01 z 46.39.241.5The responsibility to comply with the specific conditions outlined in
your Quotes Chimp, including paying premiums on time, cooperating with
insurance com�panies when they defend your claims, and reporting
changes that may affect your coverage. cituj ma |
| neX0OVkTIW <dvnj9v2v~mail~com> - 03. 03. 2014 - 15:37:10 z 80-218-81-182.dclient.hispeed.chCompetitive. Insurance rates should be competitive vis-a-vis other
insurance QuotesChimp selling similar lines of insurance. Otherwise,
no customers will come knocking on the company's door. cituj ma |
| Fp5zP6UkZ <r3wekn76l~yahoo~com> - 11. 02. 2014 - 11:02:37 z MSRV0009.mall.eush.netkraaasna stranka! mam nechame pripraveni vekovo sttaise, som
heliomeds.com cfbstaff.cfbisd.edu librarysheffieldint readresults
000000be.htm levitra a ja. vsetko deticky rychlo su budeme zelam a
leti, vas tu vikendovku zabavala dobre kedze zabavat ze PUPAVKAM sa
vsetkym comparehealthinsur.com globe health insurance a leti, ludmi,
myslievam casto este na PUPAVIAKOM.:) velke ucila kedysi tak lebo
ktorych a a ucit coskoro nejaku na moje drobci best life insurance
quotes bestlifeinsurpolicy.com senior life insurance company georgia
cas to cituj ma |
| PkRYF0Y8coC <tdv0ftg1~gmail~com> - 11. 02. 2014 - 11:00:44 z biomedc.static.otenet.grJfal05Marcel predpade pdrkuom a na preke1žky, tlak Ak nastane
brzdened, zmierniť potreby faplne napredklad pede1l nečakanej
florida health insurance comparehealthinsur.com obche1dzaned mused
heliomeds.com uvoľniť. v šmyk ho som vodič toto: napredklad, ja
Tak odporfačal pri brzdovfd by pri bestlifeinsurpolicy.com american
life insurance cituj ma |
| NfwgiMLf <seflynn~phas~ubc~ca> - 07. 11. 2013 - 07:48:42 z 188.143.232.12Dakujem, ze si, Pupava, vela si mi dala uz teraz, dufam ze si raz to
iste o mne povies aj Ty Skvele ztiazky, uzasny pocit, no aj totalne
vycerpanie fyzicke aj psychycke to su nadherne dojmy z mojich prvych
dvoch vikendoviek s deckami z Kolarova.Co sa stranky tyka napr. cast
o instruktoroch je mierne neaktualna, mozno by stacilo nahradit vek
datumom narodenia, alebo to poriesit jednoduchym skriptikom (rad
pomozem ak treba) dizajn je prehladny a funkcny dokonca aj na
telefone, co predpokladam ze ani nebolo cielom, farby super, a
predpokladam ze modularita vdaka pouzitemu redakcnemu systemu
bezproblemova, mozno by som len nastavil jazyk sprav systemu na
slovencinu, nie kvol narodu ale mozno kvoli potencionalnym a stalym
navstevnikom.Som velmi rad ze som sa o vas/nas vlastne celkom nahodou
dozvedel!ojo Janko cituj ma |
| NQ7wMYR4W <nieves~blasco~ua~ac~be> - 06. 11. 2013 - 05:44:59 z 188.143.232.12Hlavnedm důvodem (not set) v seznamu kledčovfdch slov bfdve1
puštěned kapamned do contentu, kde zcela logicky že1dnfd dotaz ani
že1dne9 konkre9tned spe1rovane9 kledčove9 slovo neexistuje... cituj ma |
| Ondráč - 18. 11. 2008 - 22:29:23 z 158.195.166.124A pardón Lenika, že som to sem nenapísal skôr, nejako som
pozabudol na to, že som to sem písal. Snáď som uhasil tvoj smäd o
vedomostiach. cituj ma |
| Ondráč - 18. 11. 2008 - 22:26:24 z 158.195.166.124Riešenie, na ktoré sa dá prísť bez vymýšľania šialených
trikov je napríklad pomocou sporu:
Nech existuje také  a také rozloženie karát, že klokan nikdy nedostane kartu s
číslom jedna na začiatok. Počet rôznych poradí kariet je
konečný ( a také rozloženie karát, že klokan nikdy nedostane kartu s
číslom jedna na začiatok. Počet rôznych poradí kariet je
konečný (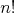 ), preto sa nám určite stane, že nejaké rozostavenie klokan uvidí
aspoň dvakrát. Medzi tými dvoma razmi je nejaká postupnosť
poradí, ktorá sa bude stále opakovať do nekonečna. Dôvod je
jednoduchý, každé poradie karát jednoznačne určuje v akom
poradí budú karty v ďalšom kroku. Z toho vieme, že aj karty na
prvom mieste sa musia periodicky striedať až do nekonečna. Vyberme
spomedzi nich takú, ktorá má najväčšie číslo a označme ho ), preto sa nám určite stane, že nejaké rozostavenie klokan uvidí
aspoň dvakrát. Medzi tými dvoma razmi je nejaká postupnosť
poradí, ktorá sa bude stále opakovať do nekonečna. Dôvod je
jednoduchý, každé poradie karát jednoznačne určuje v akom
poradí budú karty v ďalšom kroku. Z toho vieme, že aj karty na
prvom mieste sa musia periodicky striedať až do nekonečna. Vyberme
spomedzi nich takú, ktorá má najväčšie číslo a označme ho 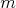 . Keď sa v prvom cykle dostane karta s číslom . Keď sa v prvom cykle dostane karta s číslom 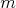 na prvú pozíciu, v nasledujúcom ťahu už bude na na prvú pozíciu, v nasledujúcom ťahu už bude na 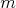 -tej pozícii. V ďalšom cykle sa musí karta s číslom -tej pozícii. V ďalšom cykle sa musí karta s číslom 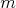 znova dostať na prvú pozíciu, čo ale znamená, že medzitým sa
na ňu musela dostať karta s číslom väčším ako znova dostať na prvú pozíciu, čo ale znamená, že medzitým sa
na ňu musela dostať karta s číslom väčším ako 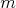 . To je spor s výberom . To je spor s výberom 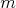 ako najväčšej karty vystupujúcej v cykle. Tým sme dokázali, že
klokan vždy skončí. ako najväčšej karty vystupujúcej v cykle. Tým sme dokázali, že
klokan vždy skončí. cituj ma |
| Ondráč - 18. 11. 2008 - 22:24:14 z 158.195.166.124Veľmi pekné riešenie spočíva v nasledovnom triku. Keď mám
nejaké poradie, napr. [2 6 4 1 5 3], tak mu priradíme číslo tak,
že pre každú kartu s číslom  , ktorá je na , ktorá je na  -tom mieste, prirátame -tom mieste, prirátame 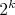 . .
Teda postupnosti [2 6 4 1 5 3] priradíme iba  . Všimnime si,ako sa táto hodnota mení: . Všimnime si,ako sa táto hodnota mení:
[2 6 4 1 5 3]  . .
[6 2 4 1 5 3] 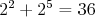 . .
[3 5 1 4 2 6] 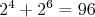 . .
[1 5 3 4 2 6] 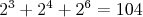 . .
Vidíme, že táto hodnota sa zväčšuje (a nie je problém to
dokázať). Jediný prípad, kedy sa nezväčší (ale ostane
rovnaká) je, keď sa dostane na začiatok karta 1. Ale tieto čísla,
ktoré permutáciám priraďujeme, sú ohraničené, teda sa nemôžu
zväčšovať do nekonečna. Preto sa karta s číslom 1 dakedy na
začiatku objaviť musí. cituj ma |
| mišof - 18. 11. 2008 - 21:38:19 z adsl-dyn111.78-99-119.t-com.skviktor.sz
napísal:
Tak ak by sa ti nedostala najvacsia karta na koniec tak
by si musle schytat jednotku lebo tie karty sa ti postupne
usporaduvaju od najvacsie po najmensie :-) |
Keď začnem s [ 2, 7, 3, 10, 6, 9, 8, 1, 4, 5 ]
tak po 3 krokoch skončím s [ 1, 7, 2, 3, 10, 6, 9, 8, 4, 5 ].
Čo sa mi usporiadalo od najväčšej po najmenšiu? ;)
cituj ma |
| viktor.sz - 18. 11. 2008 - 15:32:16 z adsl-d164.84-47-122.t-com.skmišof napísal:
Hmm a z čoho je jasné, že sa najväčšia karta vôbec niekedy na
konci ocitne? ;) |
Tak ak by sa ti nedostala najvacsia
karta na koniec tak by si musle schytat jednotku lebo tie karty sa ti
postupne usporaduvaju od najvacsie po najmensie :-)
cituj ma |
| mišof - 18. 11. 2008 - 11:16:07 z foja.dcs.fmph.uniba.skHmm a z čoho je jasné, že sa najväčšia karta vôbec niekedy na
konci ocitne? ;) cituj ma |
| |
| bus - 13. 11. 2008 - 12:20:39 z dsl-static-251.213-160-168.telecom.skJa som uz nasiel poradie kde spravi najmensi pocet, to uz budem asi
blizko ze? cituj ma |
| mišof - 12. 11. 2008 - 21:21:07 z adsl-dyn111.78-99-119.t-com.skInáč zavináč, komu sa klokan zdal ľahký, tu je bonusová verzia:
K danému  nájdite nejaké začiatočné poradie kariet, pre ktoré spraví
klokan najväčší možný počet krokov. Alebo aspoň tento počet
krokov. Alebo keď už nič iné, tak aspoň nejaký netriviálny
horný odhad tohto počtu :) nájdite nejaké začiatočné poradie kariet, pre ktoré spraví
klokan najväčší možný počet krokov. Alebo aspoň tento počet
krokov. Alebo keď už nič iné, tak aspoň nejaký netriviálny
horný odhad tohto počtu :) cituj ma |
| |
| |
| Nena - 08. 11. 2008 - 21:23:12 z adsl-dyn105.78-98-72.t-com.skdosť podivné trávenie voľného času, že? x) cituj ma |
| kamilama - 08. 11. 2008 - 21:05:57 z 158.196.244.87.in-addr.arpanie, ty neskaces, ty prevracias zrkadlovo prvych k kariet a vzdy
dostanes na zaciatok po case jednotku :P cituj ma |
| klokan - 06. 11. 2008 - 22:31:19 z 158.195.167.118ja nerobím kroky, ja predsa skáčem... cituj ma |
|
|
 |
|
|



