Zadanie:
Ondro a Feráč majú nekonečnú šachovnicu a hrávajú na nej
nasledovnú hru. Každý hráč ovláda jedného koňa, Ondrejov
začína na políčku 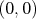 , Feráčov na , Feráčov na 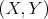 . Hráči sa striedajú v ťahoch, prvý ťahá Feráč. V jednom
ťahu je dovolené spraviť ľubovoľný (nenulový) počet
normálnych šachových krokov pre koňa, všetky však musia byť
presne v tom istom smere a vzájomná euklidovská vzdialenosť medzi
oboma koňmi sa musí každým krokom zmenšiť. Hráč prehrá vtedy,
keď nemôže spraviť žiadny krok. Predpokladajte, že obaja hráči
hrajú optimálne. Kto vyhrá? . Hráči sa striedajú v ťahoch, prvý ťahá Feráč. V jednom
ťahu je dovolené spraviť ľubovoľný (nenulový) počet
normálnych šachových krokov pre koňa, všetky však musia byť
presne v tom istom smere a vzájomná euklidovská vzdialenosť medzi
oboma koňmi sa musí každým krokom zmenšiť. Hráč prehrá vtedy,
keď nemôže spraviť žiadny krok. Predpokladajte, že obaja hráči
hrajú optimálne. Kto vyhrá? |



