Zadanie:
Nech 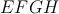 , , 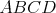 , , 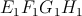 sú tri konvexné štvoruholníky zároveň spĺňajúce obe
nasledujúce podmienky:
\begin{enumerate}
\item[(i)]
Body sú tri konvexné štvoruholníky zároveň spĺňajúce obe
nasledujúce podmienky:
\begin{enumerate}
\item[(i)]
Body 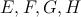 ležia postupne na stranách ležia postupne na stranách 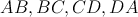 tak, že platí tak, že platí
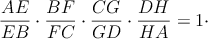
\item[(ii)]
Body 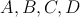 ležia postupne na stranách ležia postupne na stranách 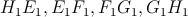 . Navyše . Navyše 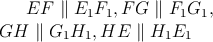 .
\end{enumerate}
Označme .
\end{enumerate}
Označme 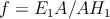 . Vyjadrite pomer . Vyjadrite pomer 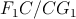 ako funkciu jedinej premennej ako funkciu jedinej premennej 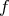 . . |



