Zadanie:
Máme dané štyri body 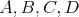 . Ľubovoľné dve kružnice také, že jedna prechádza bodmi . Ľubovoľné dve kružnice také, že jedna prechádza bodmi 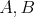 a druhá prechádza bodmi a druhá prechádza bodmi 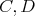 , sa pretínajú. Ak sa tieto kružnice pretínajú práve v dvoch
bodoch, označíme tieto body , sa pretínajú. Ak sa tieto kružnice pretínajú práve v dvoch
bodoch, označíme tieto body 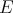 a a 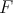 . Dokážte, že existuje bod . Dokážte, že existuje bod 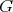 taký, aby pre všetky možné dvojice bodov taký, aby pre všetky možné dvojice bodov 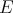 a a 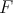 ležia body ležia body 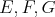 na priamke. na priamke. |



