Zadanie:
Ďalšie ráno sa Monty potichu vyplížil zo spiaceho táboriska
a vybral sa na dlhú cestu do New Orleans. Mal v pláne tam
nastražiť pascu na Drzohubých a dostať ich za mreže.
Rozhodol sa, že sa cestou zastaví v indiánskej osade kmeňa
Geometrov a poprosí tam o pomoc svojho kamaráta Sinetua.
Spoločne určite vymyslia ako banditov dolapiť. Len čo dorazil do
osady, stretol miestneho geometra Rysueta, ktorý sa opäť pasoval
s geometrickým problémom. Na zemi mal nakreslenú kružnicu  so stredom so stredom 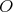 . Dnu v kruhu vymedzenom kružnicou . Dnu v kruhu vymedzenom kružnicou  ležal bod ležal bod 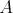 a mimo tohto kruhu ležal bod a mimo tohto kruhu ležal bod 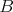 . Navyše platilo, že body . Navyše platilo, že body 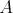 , , 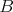 a a 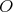 neležia na jednej priamke. Rysueto chcel nájsť všetky
priesečníky priamky určenej bodmi neležia na jednej priamke. Rysueto chcel nájsť všetky
priesečníky priamky určenej bodmi 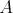 a a 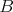 a kružnice a kružnice  . Stále mal však zapatrošené svoje pravítko, a tak mal
k dispozícii iba kružidlo. Do neho vie nabrať vzdialenosť
medzi ľubovoľnými dvoma narysovanými bodmi a nakresliť
kružnicu s nabraným polomerom a ľubovoľným stredom.
Pomôžte Rysuetovi nájsť všetky priesečníky priamky . Stále mal však zapatrošené svoje pravítko, a tak mal
k dispozícii iba kružidlo. Do neho vie nabrať vzdialenosť
medzi ľubovoľnými dvoma narysovanými bodmi a nakresliť
kružnicu s nabraným polomerom a ľubovoľným stredom.
Pomôžte Rysuetovi nájsť všetky priesečníky priamky 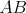 a kružnice a kružnice  len za pomoci kružidla a vášho umu. Nezabudnite, že bez
pravítka neviete rysovať rovné čiary. len za pomoci kružidla a vášho umu. Nezabudnite, že bez
pravítka neviete rysovať rovné čiary.
|



