Zadanie:
Sinetu a Monty po dlhej púti konečne dorazili do New Orleans
a ihneď vyhľadali miestneho šerifa. Povedali mu o pláne
Drzohubých a o tom, že by ho za pomoci šerifových ľudí
radi prekazili. Šerif nechcel nič nechať na náhodu, a preto
sa rozhodol, že najskôr zistí, či on sám nie je lepší na
organizáciu celej akcie. Ako je dobre známe, tak úspech každej
akcie strážcov zákona závisí od troch kladných premenných 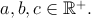 Kvalita Montyho plánu je Kvalita Montyho plánu je 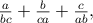 zatiaľ čo kvalita šerifovho plánu je zatiaľ čo kvalita šerifovho plánu je 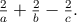 Dokážte, že Montyho plán nikdy nie je horší, t.j., že pre
všetky Dokážte, že Montyho plán nikdy nie je horší, t.j., že pre
všetky 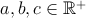 platí platí
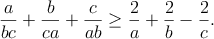
Taktiež nájdite všetky také hodnoty  , , 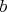 , ,  , pre ktoré nastáva rovnosť. , pre ktoré nastáva rovnosť.
|



