Zadanie:
Na každej strane rovnostranného trojuholníka 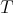 si označíme 5 bodov tak, že týchto 5 bodov rozdelí stranu na 6
rovnakých častí. Takto určených 15 bodov pospájame úsečkami
rovnobežnými so stranami trojuholníka si označíme 5 bodov tak, že týchto 5 bodov rozdelí stranu na 6
rovnakých častí. Takto určených 15 bodov pospájame úsečkami
rovnobežnými so stranami trojuholníka 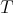 . Týmito úsečkami sme trojuholník . Týmito úsečkami sme trojuholník 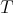 rozdelili na 36 malých rovnostranných trojuholníkov. Na každý z
28 vrcholov malých trojuholníkov položíme práve jednu žabu. V
každej sekunde každá žaba skočí na susedný vrchol. Navyše
vieme, že ak zoberieme tri pozície ľubovoľnej žaby za sebou (v
časoch rozdelili na 36 malých rovnostranných trojuholníkov. Na každý z
28 vrcholov malých trojuholníkov položíme práve jednu žabu. V
každej sekunde každá žaba skočí na susedný vrchol. Navyše
vieme, že ak zoberieme tri pozície ľubovoľnej žaby za sebou (v
časoch 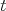 , ,  a a  ), tak tieto pozície neležia na jednej priamke (takže žaba sa
nemôže vracať, ani pokračovať vo svojom smere). Dokážte, že v
nejakom čase budú nejaké dve žaby na rovnakom vrchole. ), tak tieto pozície neležia na jednej priamke (takže žaba sa
nemôže vracať, ani pokračovať vo svojom smere). Dokážte, že v
nejakom čase budú nejaké dve žaby na rovnakom vrchole. |



