Zadanie:
Okolo okrúhleho stola sedí 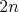 vedúcich vrátane Maťka. Medzi nimi je nejako rozdelených vedúcich vrátane Maťka. Medzi nimi je nejako rozdelených 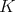 koláčov. Každý z vedúcich vlastniacich aspoň dva koláče sa
môže kedykoľvek rozhodnúť, že zje jeden zo svojich koláčov a
zároveň daruje ďalší zo svojich koláčov jednému zo svojich
susedov.
Nájdite najmenšie také koláčov. Každý z vedúcich vlastniacich aspoň dva koláče sa
môže kedykoľvek rozhodnúť, že zje jeden zo svojich koláčov a
zároveň daruje ďalší zo svojich koláčov jednému zo svojich
susedov.
Nájdite najmenšie také 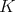 , že bez ohľadu na počiatočné rozmiestnenie koláčov ich vedúci
vedia posunúť tak, aby Maťko dostal aspoň jeden koláč. , že bez ohľadu na počiatočné rozmiestnenie koláčov ich vedúci
vedia posunúť tak, aby Maťko dostal aspoň jeden koláč.
|



