Zadanie:
Pred odchodom sa ešte Monty zastavil v svojej chatrči na kraji
mesta, aby si zbalil veci na cestu. Našiel skoro všetko čo
potreboval, no nenašiel žiadny zo svojich obľúbených polynómov.
Pre každý z Montyho obľúbených polynómov 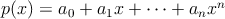 platí, že koeficient platí, že koeficient 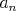 je nenulový a je nenulový a  je aspoň jedna. Ďalej platí, že všetky koeficienty je aspoň jedna. Ďalej platí, že všetky koeficienty 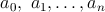 sú racionálne čísla, a že sú racionálne čísla, a že 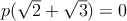 . Posledné, čo vieme o polynóme . Posledné, čo vieme o polynóme 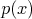 je to, že je najmenšieho možného stupňa (t.j. je to, že je najmenšieho možného stupňa (t.j.  je najmenšie možné). Nájdite aspoň jeden Montyho obľúbený
polynóm. Nezabudnite dokázať, že je najmenšieho možného
stupňa. je najmenšie možné). Nájdite aspoň jeden Montyho obľúbený
polynóm. Nezabudnite dokázať, že je najmenšieho možného
stupňa.
|



