|
|
 |
11. príklad 1. letnej série 2007/2008
Zadanie:
Kružnica, rozdelená na  oblúkov bodmi postupne pomenovanými oblúkov bodmi postupne pomenovanými 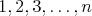 , reprezentuje hraciu arénu pre dvoch hráčov, ktorí sa striedajú
v ťahaní. V jednom ťahu si hráč vyberie dva zatiaľ voľné body
(také, ktoré ešte nie sú koncom žiadnej úsečky) s rovnakou
paritou a spojí ich úsečkou. Môže ale spojiť iba také body, aby
novovzniknutá úsečka nepretínala žiadnu z predchádzajúcich
úsečiek. Prehrá ten hráč, ktorý už nemôže spraviť ťah. Ak
obaja hráči používajú optimálnu stratégiu, ktorý z nich
vyhrá? , reprezentuje hraciu arénu pre dvoch hráčov, ktorí sa striedajú
v ťahaní. V jednom ťahu si hráč vyberie dva zatiaľ voľné body
(také, ktoré ešte nie sú koncom žiadnej úsečky) s rovnakou
paritou a spojí ich úsečkou. Môže ale spojiť iba také body, aby
novovzniknutá úsečka nepretínala žiadnu z predchádzajúcich
úsečiek. Prehrá ten hráč, ktorý už nemôže spraviť ťah. Ak
obaja hráči používajú optimálnu stratégiu, ktorý z nich
vyhrá? |
SIMONKA <NIJAKY> - 07. 11. 2008 - 14:43:20 z adsl-dyn46.78-99-220.t-com.skrasto6sk
napísal:
Ta druha verzia je naozaj zaujimava :) Odporucam skusit.
My sme to s busom skusali aj vseliakymi brute-frocami, grundyho
cilsami a inymi a naozaj sme to pre n<= asi 20 vyriesili. Ale este
som nevidel kompletne hotove riesenie, ktoremu by som uveril. Jaro,
tak ak ho mas, nemusis ho posielat sem, nech si kazdy moze skusit, ale
mne by si mohol :)
Jaro napísal:
Tá úloha mala ešte jednu trochu ťažšiu verziu, ale zostalo to
pri tejto (bol som v pokušení ukecať ostatných, aby dali verziu 2,
ale to by mi asi neprešlo, keď už túto dali na 11:(( ). Druhá
verzia je zaujímavejšia, nedá sa zriešiť len čistou symetriou.
Alebo je to zase len mojou nezaťaženosťou na kvantite...
Vo verzii 2 sú dva voľné body tie, ktoré ešte nie sú spojené
úsečkou. Vyhrávajú tí istí ľudia, ale stratégie sa líšia
(zvlášť pre 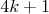 ), na párne ), na párne  sa vykašli. No a ak by sa Ti aj táto verzia nepáčila, tak sa
ospravedlňujem:( sa vykašli. No a ak by sa Ti aj táto verzia nepáčila, tak sa
ospravedlňujem:( |
|
cituj ma |
| SIMONKA <NIJAKY> - 07. 11. 2008 - 14:43:20 z adsl-dyn46.78-99-220.t-com.skrasto6sk
napísal:
Ta druha verzia je naozaj zaujimava :) Odporucam skusit.
My sme to s busom skusali aj vseliakymi brute-frocami, grundyho
cilsami a inymi a naozaj sme to pre n<= asi 20 vyriesili. Ale este
som nevidel kompletne hotove riesenie, ktoremu by som uveril. Jaro,
tak ak ho mas, nemusis ho posielat sem, nech si kazdy moze skusit, ale
mne by si mohol :)
Jaro napísal:
Tá úloha mala ešte jednu trochu ťažšiu verziu, ale zostalo to
pri tejto (bol som v pokušení ukecať ostatných, aby dali verziu 2,
ale to by mi asi neprešlo, keď už túto dali na 11:(( ). Druhá
verzia je zaujímavejšia, nedá sa zriešiť len čistou symetriou.
Alebo je to zase len mojou nezaťaženosťou na kvantite...
Vo verzii 2 sú dva voľné body tie, ktoré ešte nie sú spojené
úsečkou. Vyhrávajú tí istí ľudia, ale stratégie sa líšia
(zvlášť pre 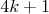 ), na párne ), na párne  sa vykašli. No a ak by sa Ti aj táto verzia nepáčila, tak sa
ospravedlňujem:( sa vykašli. No a ak by sa Ti aj táto verzia nepáčila, tak sa
ospravedlňujem:( |
|
cituj ma |
| Iustus - 15. 03. 2008 - 12:13:00 z kms.skUáá, niekto mi tu odrádza riešiteľov:) Čakal som, že prídem a
už tu budú minimálne nejaké nápady a Vy takto (vzhľadom na to,
že antismajlíky sa ešte nevymysleli, zdôrazňujem, že tu som
žiaden dať nechcel).
TomasKo., nevšímaj si ho, je to len trošku ťažšie než verzia 1.
Stačí na to stredoškolská matika. No, ja som v jednom momente
využil komponenty súvislosti, ale to bola v tej chvíli podstatne
silnejšia zbraň, než bolo treba.
2rasto6sk: Grundyho čísla, tak to znie ako atómová hlavica
(rozumej ultimátna zbraň:))). Ja som sa domnieval, že Ste to iba
hodili do PC, pozerali, čo vylezie a potom postupovali štýlom
"Poďme si my informatici pokecať o matike.":))
Ak Ťa to riešenie tak zaujíma, mohol si sa ozvať skôr. Ja som si
ho oceduľkoval ako zaujímavé, ale passé, tak som tú verziu dal
aspoň sem, nech má nejaké využitie. Takže si ma aj máličko
potešil a zato som Ti napísal kompletné riešenie (tzn., že v
skorej dobe očakávam Tvoje pripomienky;), čo pri mojom tempe zabilo
pár hodín (má to tuším dvadsať riadkov...). Celkom som sa bavil
pri písaní, zvlášť s tými Heisenbergovými úsečkami, ktoré
potenciálne existujú v každom momente a absolútne existujú práve
v jednom, ale nevieš, kde a kedy:)) Ale inak je to písané
viac-menej seriózne... hehe
Vlastne je blbé, že si medzitým sám riešenie nenašiel, lebo na
90% je zhodné s verziou 1. Dobre, tých 10% sú dve kľúčové
myšlienky (Heisenbergovky), ale tie sa zas na seba trochu
podobajú.
No a pokiaľ by si mi neveril, tak najlepším dôkazom, že si za
riešením stojím, je, že si to niekedy zahráme. Ty vyberieš
hraciu plochu a ja si potom vyberiem, či začnem:)
Ale aby si si nemyslel, že som sviňa, tak to môžeme urobiť
naopak, že si Ty vyberieš, či začneš, a ja potom vyberiem hraciu
plochu. Môžeš si vybrať;))
PS: Vzhľadom na drobné nezrovnalosti v prístupe by som sa rád
trochu uistil, že zadanie neskrýva ďaľšie dvojzmysly (riešitelia
tuším žiadne nenašli, ale čert nikdy nevie). Pre 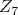 by hra mohla prebiehať takto: by hra mohla prebiehať takto: 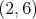 , , 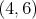 , , 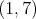 , , 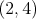 . . cituj ma |
| rasto6sk - 08. 03. 2008 - 21:47:38 z adsl-dyn67.78-99-26.t-com.skTa druha verzia je naozaj zaujimava :) Odporucam skusit. My sme to s
busom skusali aj vseliakymi brute-frocami, grundyho cilsami a inymi a
naozaj sme to pre n<= asi 20 vyriesili. Ale este som nevidel
kompletne hotove riesenie, ktoremu by som uveril. Jaro, tak ak ho mas,
nemusis ho posielat sem, nech si kazdy moze skusit, ale mne by si
mohol :)
Jaro napísal:
Tá úloha mala ešte jednu trochu ťažšiu verziu, ale zostalo to
pri tejto (bol som v pokušení ukecať ostatných, aby dali verziu 2,
ale to by mi asi neprešlo, keď už túto dali na 11:(( ). Druhá
verzia je zaujímavejšia, nedá sa zriešiť len čistou symetriou.
Alebo je to zase len mojou nezaťaženosťou na kvantite...
Vo verzii 2 sú dva voľné body tie, ktoré ešte nie sú spojené
úsečkou. Vyhrávajú tí istí ľudia, ale stratégie sa líšia
(zvlášť pre 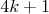 ), na párne ), na párne  sa vykašli. No a ak by sa Ti aj táto verzia nepáčila, tak sa
ospravedlňujem:( sa vykašli. No a ak by sa Ti aj táto verzia nepáčila, tak sa
ospravedlňujem:( |
cituj ma |
| Jaro - 08. 03. 2008 - 16:30:10 z kms.skbus napísal:
| nooo ale radsej si pockam
na vzorak... mozno to naozaj ma aj nejaku myslienku
:) |
Uhm, no neviem :). |
Navrhoval som ho na devinu a tu to máme, riešitelia čakali od
jedenástky peknú pointu.
2TomášKo.:Typická symetria sa ľudkom z matických tried sotva
mohla páčiť... mne sa páčila, lebo to bola asi tak piata úloha
na symetriu, ktorú som niekedy riešil, preto nie som znechutený
kvantitou. Vlastne som nikdy nebol znechutený kvantitou žiadneho
typu úloh:)) Tá úloha mala ešte jednu trochu ťažšiu verziu, ale
zostalo to pri tejto (bol som v pokušení ukecať ostatných, aby
dali verziu 2, ale to by mi asi neprešlo, keď už túto dali na
11:(( ). Druhá verzia je zaujímavejšia, nedá sa zriešiť len
čistou symetriou. Alebo je to zase len mojou nezaťaženosťou na
kvantite...
Vo verzii 2 sú dva voľné body tie, ktoré ešte nie sú spojené
úsečkou. Vyhrávajú tí istí ľudia, ale stratégie sa líšia
(zvlášť pre 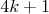 ), na párne ), na párne  sa vykašli. No a ak by sa Ti aj táto verzia nepáčila, tak sa
ospravedlňujem:( sa vykašli. No a ak by sa Ti aj táto verzia nepáčila, tak sa
ospravedlňujem:(
cituj ma |
| bus - 08. 03. 2008 - 10:13:04 z dsl-static-251.213-160-168.telecom.sk| nooo ale radsej si pockam
na vzorak... mozno to naozaj ma aj nejaku myslienku
:) |
Uhm, no neviem :).
cituj ma |
| Kubo - 07. 03. 2008 - 17:07:14 z adsl-dyn205.78-99-153.t-com.skmne sa tento priklad strasne velmi moc mrte velice nepacil lebo som az
po odoslani zistil ze tam je to s rovnakou paritou. A nevedel som to
zbusit. cituj ma |
| TomasKo. <tomas~kocak~gmail~com> - 06. 03. 2008 - 20:52:18 z nat-88-212-20-164.antik.skcaute... je to super ze pribudlo toto forum o prikladoch sa mi to paci
:) nooo a ten priklad sa mi nepacil... lebo som cakal ze to bude mat
aj nejaku pointu alebo nieco take... a namiesto toho som len rozobral
4 pripady a to bolo vsetko.. nooo ale radsej si pockam na vzorak...
mozno to naozaj ma aj nejaku myslienku :) cituj ma |
| |
| Miso <miso~ksp~sk> - 04. 03. 2008 - 20:42:24 z 188-37-16-84.mcrn.sktoto sme mali na heuristickych metodach:) velmi pekny priklad cituj ma |
| rasto <rasto6sk~yahoo~co~uk> - 04. 03. 2008 - 19:15:36 z adsl-dyn67.78-99-26.t-com.skNo som velmi zvedavy ako sa vam pacila tato uloha :) dufam, ze sa ju
podarilo viacerym uspesne vyriesit :) cituj ma |
|
|
 |
|
|



