|
|
 |
9. príklad 1. zimnej série 2010/2011
Zadanie:
Kde bolo, tam bolo, v Kráľovstve Múdrych Stvorení, slávny rytier
Eduard prezývaný Edo sa po večeroch venoval svojmu koníčku -
matematike. Jeden upršaný deň mu spríjemnila istá zvláštna
podmnožina 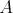 množiny čísel množiny čísel  . O tejto podmnožine sa v kráľovstve šepkalo, že mala aspoň 1003
prvkov. Táto správa sa dostala aj dvornému šašovi Mišovi. Ten po
chvíli usúdil, že množina . O tejto podmnožine sa v kráľovstve šepkalo, že mala aspoň 1003
prvkov. Táto správa sa dostala aj dvornému šašovi Mišovi. Ten po
chvíli usúdil, že množina 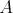 musí obsahovať aspoň jednu mocninu dvojky, alebo dve čísla,
ktorých súčet je mocninou dvojky. Dokážte, že sa nemýlil. musí obsahovať aspoň jednu mocninu dvojky, alebo dve čísla,
ktorých súčet je mocninou dvojky. Dokážte, že sa nemýlil. |
Brano - 29. 10. 2010 - 14:49:52 z 188-167-9-99.dynamic.chello.skPočkať, vy ste mi za úlohu 9 strhli bod za to, že som dôležité
tvrdenie napísal do zátvorky trochu ho nezvýraznil? Aha. cituj ma |
|
|
 |
|
|



