|
|
 |
3. príklad 3. letnej série 2008/2009
Syseľ - 18. 05. 2009 - 20:54:39 z gw-sa3.salamon.skV tom prípade ... hamba vedúcim! cituj ma |
| Michal A. - 16. 05. 2009 - 12:02:32 z adsl-d144.84-47-34.t-com.skPoprípade si myslia, že to bola banalita a neoplatí sa to ani
spomínať :-) cituj ma |
| Syseľ - 15. 05. 2009 - 22:16:12 z gw-sa3.salamon.skĽahký - neľahký, keďže sem nikto nič nepíše, znamená to, že
ho nikto okrem nás nedal :-) cituj ma |
| Michal A. - 12. 05. 2009 - 18:35:54 z adsl-dyn-45.95-102-8.t-com.skTo bol jeden z najkrajších príkladov :) cituj ma |
| Sysel - 07. 05. 2009 - 20:53:09 z gw-sa3.salamon.skCela finta spocivala v tom, ze 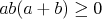 ! !
Potom to uz boli iba primitivne upravy smerujuce od (pre niektorych
k) 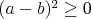 . .
Take krasne a jednoduche ! cituj ma |
|
|
 |
|
|



