kms - fórum o príkladoch

fórum o príkladoch

korešpondenčný matematický seminár

5. príklad 3. letnej série 2008/2009

Zadanie:
Existujú prirodzené čísla $a,b,c$ tak, aby obidva korene rovnice

$\pm ax^2 \pm bx \pm c = 0$

boli pre ľubovoľný výber znamienok celé čísla?

Naspäť na príklady | Napíš príspevok

FEki5bvo <umwbshi1gq~mail~com> - 21. 10. 2015 - 12:53:23 z 221.178.182.20

I`m so grateful that you elngihtened me and the most important thing that it happened in time. Just think, I have been using the internet for six years already but it`s the first time I`ve ever heard about it!

Syseľ - 19. 05. 2009 - 21:27:17 z gw-sa3.salamon.sk

V tom prípade sú všetky výroky platné! :-)

Linda - 19. 05. 2009 - 12:44:16 z router.gjh.sk

Bus to pochopil, len ja sa neviem vyjadrovat :D

Bus - 19. 05. 2009 - 00:49:12 z dsl-static-251.213-160-168.telecom.sk

No podla mna to Linda myslela tak, ze

"Plny pocet si nedostala preto, ze si nespravila skusku spravnosti, alebo si nedostala plny pocet bodov preto, ze si nieco zle napisala."

Syseľ - 18. 05. 2009 - 20:52:38 z gw-sa3.salamon.sk

Linda napísal:
syslik, preto som tam dala dve moznosti, bud si nedala skusku, alebo si nieco zle napisala :P

Milá Linda, uvažujme situáciu, že by niekto nespravil skúšku ale mal príklad dobre. Potom by podľa tvojho výroku bola splnená jedna podmienka disjunkcie a tým pádom by bol platný celý výrok, ktorý podľa syntaxu článku implikuje výrok "Nedostal(a) som plný počet bodov."
Keďže som skúšku nespravil a plný počet bodov mám je tvoj výrok v rozpore s konaním vedúcich pri konkrétnom príklade. Keďže vedúci majú na tomto fóre vždy pravdu, tvoj výrok je neplatný.
Týmto som tiež dokázal, že môj výrok:

Sysel napísal:
...Linda, Ani ty nemáš úplnú pravdu (nie, že by si ju namala Vždy... ). O skúške som tam nenapísal ani čiarku (teda, aspoň si nepamätám) mám 9 bodov...
je platný!

Linda - 16. 05. 2009 - 15:01:34 z dial-95-105-130-158-orange.orange.sk

syslik, preto som tam dala dve moznosti, bud si nedala skusku, alebo si nieco zle napisala :P

Sysel - 15. 05. 2009 - 22:14:17 z gw-sa3.salamon.sk

Michal, dobrý vtip!
Linda, Ani ty nemáš úplnú pravdu (nie, že by si ju namala Vždy... ). O skúške som tam nenapísal ani čiarku (teda, aspoň si nepamätám) mám 9 bodov.
Baša, nič si z toho nerob. AJ GÉNIUS SA SEKNE

Linda S. - 14. 05. 2009 - 21:42:21 z dial-95-105-130-158-orange.orange.sk

Michal A. napísal:

Baša K. napísal:
prečo som dostala len 5 bodov???...veď som našla dokonca 5 riešení....:(

Možno preto, že si nenašla všetky :)

to je blbost, ja som dala iba jednu trojicu a dostala som celych 9 bodov, mozno si nespravila skusku spravnosti alebo si nieco zle napisala

Michal A. - 14. 05. 2009 - 21:31:50 z adsl-d150.84-47-72.t-com.sk

Baša K. napísal:
prečo som dostala len 5 bodov???...veď som našla dokonca 5 riešení....:(

Možno preto, že si nenašla všetky :)

Sysel - 14. 05. 2009 - 19:31:17 z gw-sa3.salamon.sk

Basha napísal:
Sysel skus to napisat aby som tomu pochopila aj ja... daj k tomu este kus reci... :D

Vlastne to znamena iba tolko, ze ak chces nejaku taku trojicu najst, dosadis za cisla $a, d, e$ lubovolne prirodzene cisla a podla vyrazov si vypocitas $b$ a $c$ .
Korene, ktore ti potom mozu vyst ziskas tak,
ze do vyrazov v mnozine dosadis hodnotu $e$ (tu istu ktoru si dosadzovala predtym) a potom si vyberies jeden vyraz z mnoziny, ktory dosadis za $m$ cim ziskas dva korene. Kedze vyrazy su 4, korenov je 8.
POCHOPILA?

Sysel - 14. 05. 2009 - 19:20:02 z gw-sa3.salamon.sk

Linda S. napísal:
kedze staci ak dokazene ci existuju take prirodzene cisla a,b,c... blablabla... stacilo nam najst jednu dvojicu pri kt. to plati a skuska spravnosti. a ja som nasla a=1 b=5 c=6. Sysel, to tvoje som ani pouzit nemusela :), ale dufam ze mi to uznaju

Ak si dosadis 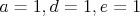$a = 1, d = 1, e = 1$ vide ti to iste. Ale nemusis sa bat, tvoje riesenie by teoreticky malo byt spravne. Ja som to napisal iba preto aby som tychto ludi zmiatol...
Ale aj tak je to najkomplexnejsie riesenie...

Baša K. - 14. 05. 2009 - 18:58:42 z adsl-dyn38.78-98-147.t-com.sk

prečo som dostala len 5 bodov???...veď som našla dokonca 5 riešení....:(

Basha - 13. 05. 2009 - 19:17:25 z 85-135-202-143.3pp.slovanet.sk

Sysel skus to napisat aby som tomu pochopila aj ja... daj k tomu este kus reci... :D

Linda S. - 12. 05. 2009 - 19:15:40 z dial-92-52-28-246-orange.orange.sk

kedze staci ak dokazene ci existuju take prirodzene cisla a,b,c... blablabla... stacilo nam najst jednu dvojicu pri kt. to plati a skuska spravnosti. a ja som nasla a=1 b=5 c=6. Sysel, to tvoje som ani pouzit nemusela :), ale dufam ze mi to uznaju

Michal A. - 12. 05. 2009 - 18:42:35 z adsl-dyn-45.95-102-8.t-com.sk

Tomu tvojmu Sysel nerozumiem, ale ja som na to isiel caz Vietove vztahy. Dufam ze to budem mat dobre :)

Baša K. - 11. 05. 2009 - 19:18:04 z adsl-dyn38.78-98-147.t-com.sk

popravde som na to kukala jak kukala, aj tak som envedela co tam je napisane...(mne to tak trochu vypocital pocitac)...

Sysel - 09. 05. 2009 - 20:26:58 z gw-sa3.salamon.sk

Znamena to ze ak za a,d,e dosadis co chces, rovnica s danymi koeficientami ma vzdy celociselne riesenia!
Skus to!

Nena - 08. 05. 2009 - 20:45:55 z adsl-dyn9.78-98-176.t-com.sk

Chjo, Syseľ, ale ja tomu tvojmu riešeniu nerozumiem, ani keď naňho zíram tri minúty v kuse a snažím sa ho pochopiť :D No jó, vidno, vďaka komu sme ten druboj na alfe vyhrali :)

Sysel - 08. 05. 2009 - 19:16:10 z gw-sa3.salamon.sk

Aky sialenec ?! ... primitivna matika

Nena - 08. 05. 2009 - 09:43:42 z adsl-dyn9.78-98-176.t-com.sk

nfvhf?? šialenec :D

Sysel - 07. 05. 2009 - 21:19:23 z gw-sa3.salamon.sk

Som si isty, ze kazdy prisiel na to, ze ak:
$a = a$ ,
$b = ad(2e^2 + 2e + 1)$ ,
$c = ad^2e(2e^2 + 3e + 1)$ ,
kde $a, d, e \in \Bbb N$ ,
tak rovnica ma vsetky riesenia celociselne, pricom ich tvar je $x = \pm dm$ ,
kde $m \in \{e, e + 1, 2e^2 + e, 2e^2 + 3e + 1\}$
$:-)$

úvod | zadania | poradie | vzoráky | debata | sústredenia | výlety