|
|
 |
9. príklad 2. letnej série 2013/2014
Zadanie:
Máme 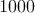 normálnych mincí, z ktorých každá váži normálnych mincí, z ktorých každá váži 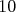 gramov a gramov a 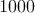 falošných, z ktorých každá váži falošných, z ktorých každá váži 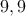 gramu. Máme k dispozícii superpresné dvojramenné váhy.
Potrebujeme spraviť dve kôpky mincí, pričom v oboch je rovnaký
počet mincí, no súčet hmotností mincí v týchto kôpkach je
rôzny. Koľko najmenej vážení potrebujeme na to, aby sme s istotou
vedeli takéto dve skupiny nájsť? gramu. Máme k dispozícii superpresné dvojramenné váhy.
Potrebujeme spraviť dve kôpky mincí, pričom v oboch je rovnaký
počet mincí, no súčet hmotností mincí v týchto kôpkach je
rôzny. Koľko najmenej vážení potrebujeme na to, aby sme s istotou
vedeli takéto dve skupiny nájsť?
|
5sLc2XiActu <hmyyzvlesf~yahoo~com> - 26. 12. 2015 - 16:56:05 z mail.mccarthy-bush.comHmm, bez toho aby som sa dlhsie zasymlal, mam otazku: ked sa robi ten
vybuch, ako sa vybera ta dvojica ktoru odstranime?Cakal by som, ze v
povodnej Ondracovej verzii bolo ze vyberiem nahodnu susediacu dvojicu.
Ale ta Radova verzia sa da chapat (aj) tak, ze vyberiem nahodneho
diktatora a ten vyberie nahodneho ziveho suseda a napadne ho. Toto
robi inu distribuciu -- totiz tie dvojice, kde uz jedna planeta ma len
jedneho suseda budu pravdepodobnejsie ako tie dvojice ktore su este
niekde v strede suvisleho useku.Inak som pre tu prvu (uniformnu)
verziu teda dospel k podobnemu ako uz Ondro napisal. Nech je prva
znicena dvojica hociktora, vzdy dostaneme rad tvoreny N-2 planetami.
No a ked si oznacime R_x ocakavany pocet toho co nam ostane z radu
dlzky x, tak dostavame taku rekurenciu zeR_x = \frac{1}{x-1} \cdot
\sum_{l=0}^{x-2} ( R_l + R_{x-2-l} )z coho upravou dostaneme nieco
takmer rovnake ako ten prvy Ondrov vzorec. A potom riesenie E_n =
R_{n-2}. cituj ma |
|
|
 |
|
|



