|
|
 |
8. príklad 1. letnej série 2007/2008
Zadanie:
Peťko hodil 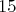 -krát mincou a zapísal si postupnosť hláv a znakov, ktorá mu
padla. Potom zrátal počet dvojíc hlava-hlava, hlava-znak,
znak-hlava, znak-znak, ktoré padli v dvoch po sebe idúcich hodoch.
Vyšli mu postupne počty -krát mincou a zapísal si postupnosť hláv a znakov, ktorá mu
padla. Potom zrátal počet dvojíc hlava-hlava, hlava-znak,
znak-hlava, znak-znak, ktoré padli v dvoch po sebe idúcich hodoch.
Vyšli mu postupne počty 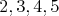 . Koľko je rôznych postupností, ktoré môže mať Peťko
zapísané? . Koľko je rôznych postupností, ktoré môže mať Peťko
zapísané? |
Mustang - 27. 03. 2008 - 15:03:04 z static-081-022-141.dsl.nextra.skpravda pravda, v mojom rieseni kombinacne cislo nebolo len
spocitavanie a nasobenie a nestrhli mi body. cituj ma |
| Zuska - 16. 03. 2008 - 20:17:33 z 158.195.164.235ahoj, v rieseni samozrejme nebolo nutne pouzit zlomky bez zlomkovej
ciary (kombinacne cisla). ak mas 6 bodov, je to sposobene niecim inym
(chyba vo vypoctoch, nedostatocna argumentacia a podobne chmary).
tento priklad sa naozaj dal zratat s vedomostami zo zs ako scitavanie
a nasobenie a krutou logikou, za to sme urcite nikomu nic nestrhavali. cituj ma |
| kamilama - 13. 03. 2008 - 17:09:50 z 158.196.244.87.in-addr.arpazuska a co s nami ktori namaju ani paru co znamenaju tie zlomky bez
zlomkovej ciary lebo kombinatoriku sa nemali odkial naucit? ale vazne
na zs to bolo nepovinne ucivo alebo to bolo vzdy tak ku koncu roka a
nikdy sme to nebrali. a teraz na strednej - no este sme sa k tomu
nedostali. a tk som nerobila moje riesenie cez tie ciselka take ale
preco mam iba 6? cituj ma |
| mito - 11. 03. 2008 - 11:44:16 z proxy.uniba.skZuska napísal:
2Zoltan: ahoj, dik za reakciu, inak to by aj mna zaujimalo. pekny
den! |
2zoltan, zuska: podla mna je to tym, ze je taky skvely ten vzorak, ze
niet co dodat :).
Navyse Zuska s Buggom boli bezkonkurencne prvy kto sem spachal vzorak
a za to si zasluzia velku pochvalu a cokoladu, najlepsie od Busa ;)
cituj ma |
| Zuska - 10. 03. 2008 - 22:24:15 z 158.195.162.1712Zoltan: ahoj, dik za reakciu, inak to by aj mna zaujimalo. pekny den! cituj ma |
| Zoltán - 10. 03. 2008 - 22:21:35 z 158.195.164.235Ahoj Zuska. Tento vzorák je úplne super, len škoda tých preklepov.
Nerozumiem len, prečo na neho nikto nereaguje. cituj ma |
| zuska & buggo - 04. 03. 2008 - 20:50:52 z 158.195.168.244Predbezny vzorak:
Milé deťúrence a iné žubrienky. Tento vzorák sa skladá z dvoch
častí. V prvej objasňujeme základné myšlienky a prístupy,
ktoré by mohli viesť k riešeniu. Druhá časť obsahuje priame
riešenie bez zbytočných rečí navyše.
V riešení bude h označovať hlavu, o orla a z
znak. Vypíšme si niekoľko postupností pĺňajúce zadanie a
pozrime sa na ne. Existuje nejaký súvis medzi výskytmi dvojíc
hz a zh, alebo ich počtami? Po krátkom hraní sa a
hľadaní skrytých vlastností si všimneme, že medzi dvoma
hz je nutne jedno zh a naopak. My máme tri hz a
štyri zh, čo znamená, že na začiatku bude určite z
a na konci h (premyslite si prečo). Napíšme si teraz
postupnosť zhzhzhzh. Keď teraz namiesto nejakého z
napíšeme postupnosť viacerých zetiek, počet dvojíc
zz nám primerane narastie (pridám dve z, pribudnú dve
dvojice). Takže nás zaujíma, koľkými spôsobmi môžeme rozdeliť
päť zetiek na štyri miesta a dve háčka na ďalšie
štyri miesta. Aby se to zrátali, môžeme použiť staré známe
úvahy o chlievikoch a oddeľovačoch, známe tiež pod názvom
kombinácie s opakovaním. Keďže každé rozdelenia z možno
skombinovať s každým rozdelením h sú navzájom
nezávislé, vynásobením týchto dvoch čísel dostaneme hľadané
riešenie. Výsledok je teda
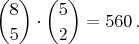
Tu je už sľúbená druhá časť, čisté riešenie. Označme
ZHZHZHZH každú postupnosť zloženú z písmen z a
h takú, že každé z (resp. h) predstavuje
niekoľko (aspoň jedno) písmen z (resp. h). V takejto
postupnosti budú vždy práve tri dvojice hz a práve štyri
dvojice zh. Teda nami požadované postupnosti budú určite v
tomto tvare.
Ak chceme, aby počet dvojíc zz bol 5, musia sa tieto dvojice
vyskytovať vrámci niektorých blokov z. Jeden blok z,
pozostávajúci z k písmen z, obsahuje k-1
dvojíc zz. Nakoľko z obsahuje vždy aspoň jedno
písmeno z, všetkých možných rozložení dvojíc zz
je rovnako veľa ako možností rozloženia 5 prvkov do 4 priehradok,
teda
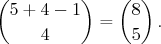
Analogickým postupom pre hh dostaneme výsledok
 .
Nakoľko rozdelenie zz a hh je nezávislé, výsledný
počet postupností je .
Nakoľko rozdelenie zz a hh je nezávislé, výsledný
počet postupností je
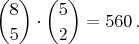
cituj ma |
|
|
 |
|
|



